§ 17. Примеры конструктивных представлений величин

Рассмотрим линейный порядок. Знания Т о линейном порядке содержат аксиомы антисимметричности, полноты и транзитивности. Линейными порядками являются, например, балльные величины и величины типа «число»: число рабочих на предприятии, число автокатастроф, число браков или разводов и т. д. Значениями многих таких величин являются натуральные числа, поэтому их естественным числовым представлением может быть конструктивное числовое представление. Такие величины удовлетворяют следующей аксиоме.

Аксиома Т1. Любая ограниченная сверху (снизу) последовательность a₁ < a₂ < a₃ < … < a (a < … < a₃ < a₂ < a₁) конечна.

Обозначим теорию линейного порядка вместе с аксиомой Т1 через T1. Известно, что любой линейный, но не более чем счетный порядок, удовлетворяющий теории T1, вложим в модель áw; £ñ. Отсюда следует решение проблемы существования конструктивного числового представления для линейных порядков T1.

Предложение 1. Любой линейный порядок Á Î AC_w(T₁) имеет конструктивное числовое представление.

Конструктивными числовыми представлениями могут служить обычные способы нумерации значений этих величин.

Рассмотрим линейные порядки, удовлетворяющие аксиоме полноты.

Аксиома Т2. "a, b, $c(a < c < b).

Обозначим через Т2 теорию линейного порядка вместе с аксиомой Т2. Примерами полных линейных порядков, удовлетворяющих Т2, являются физические величины, используемые в нефизических областях. Например, величины температуры, давления, веса человека, рассматриваемые с медицинской точки зрения, или температуры, освещенности, влажности почвы, рассматриваемые с сельскохозяйственной точки зрения. Для этих величин операция сложения (имеющая смысл с физической точки зрения) смысла не имеет. Осмысленно только отношение порядка, являющееся полным линейным порядком. Такой порядок естественно представлять не действительными, а рациональными числами. Получим конструктивное числовое представление полных линейных порядков, используя рациональные числа. Известно, что любой полный, не более чем счетный линейный порядок Á Î AC_w(T2) изоморфен одному из интервалов (0, 1), [0, 1), (0, 1], [0, 1] множества рациональных чисел.

Предложение 2. Любой полный линейный порядок Á Î AC_w(T2) имеет конструктивное числовое представление.

Примерами конструктивных числовых представлений могут служить градации шкал приборов, измеряющих эти величины.

Рассмотрим деревья – рефлексивные, антисимметричные, транзитивные порядки, удовлетворяющие следующей аксиоме.

Аксиома Т3. "a, b, c( c £ a & c £ b Þ a £ b Ú b £ a ).

Обозначим теорию деревьев через Т3. Конечными деревьями описываются такие величины, как должность, занимаемое место (в дереве рабочих мест некоторой организации), иерархические величины и т. д. 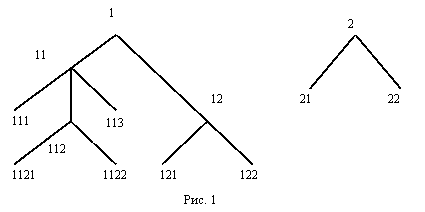Конечные деревья всегда конструктивизируемы, поэтому решение проблемы существования конструктивного числового представления сводиться к построению простой и удобной конструктивизации, применимой к любому конечному дереву. Пример такого конструктивного числового представления приведен на рис. 6.

Если у дерева несколько корневых вершин, то они нумеруются числами 1, 2, 3, ... Вершинам дерева (значениям величины) сопоставляются наборы натуральных чисел a = n(án^a₁, …,  n^a_kñ), b = n(án^b₁, …,  n^b_mñ). По числам из набора легко определяется отношение порядка между a и b.

Шкалы m : Á ® Â практически реализуются в виде шкал приборов (весов, линейки, термометра). Конструктивизации n также могут реализовываться как показания некоторых измерительных процедур, в частности тестирования, анкетирования, обследования и т. д.

Предположим, что нас интересует отношение предпочтения некоторой величины Á = áA; £ñ (коэффициента интеллектуальности, удовлетворенности работой, температура) и способ прямого измерения отношения предпочтения £ дорог, неудобен, требует большого времени и т. д. Для более простого и быстрого измерения этого отношения разрабатывается и используется тест (анкета, обследование). Применение теста к испытуемому (респонденту, больному) дает для некоторого значения a Î A величины Á набор ответов в виде некоторой последовательности натуральных или рациональных чисел án^a₁, …,  n^a_kñ. Если по результатам теста для любых двух значений a, b Î A величины Á можно эффективно определить отношение предпочтения

a £ b Û P^N(án^a₁, …,  n^a_kñ, án^b₁, …,  n^b_lñ)

например, подсчитывая сумму баллов, взвешенное среднее, кодировать ответы и т. д., то отображение Á : án^a₁, …,  n^a_kñ ® a, осуществляемое тестом будет конструктивным числовым представлением величины Á = áA; £ñ. Сама процедура тестирования (анкетирования, обследования) будет конструктивной измерительной процедурой со значениями вида án^a₁, …,  n^a_kñ.

Примером такого отношения предпочтения и соответствующего теста является отношение предпочтения между односемейными домами [54; с. 243].

Использование теста для конструктивного измерений некоторой величины может быть обосновано решением следующей задачи. Пусть задано некоторое отношение предпочтения £ величины Á = áA; £ñ, обладающее свойствами Т (удовлетворяющее аксиомам частичного порядка, толерантности, решеток). Требуется решить проблему существования конструктивного числового представления n для любой величины Á Î AC_w(T) и затем для данной нам величины Á разработать тест, измеряющий ее конструктивное числовое представление n. Мы не можем сразу строить конструктивное числовое представление n для исходной величины Á, так как она известна нам только своими аксиомами, содержащимися в Т. Поэтому решить проблему существования конструктивного числового представления нужно опираясь на AC_w(T).