|
Text in pdf-file
mcf.pdf
Потоком в ориентированном графе
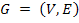 из
вершины-источника из
вершины-источника
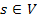 в
вершину-сток в
вершину-сток
 называется
неотрицательная функция называется
неотрицательная функция
 такая,
что для каждой вершины такая,
что для каждой вершины
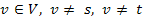 выполняется выполняется

Значение

является величиной потока из
 в в
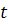 . .
Пусть
 —
набор путей (простых цепей) из из —
набор путей (простых цепей) из из
 в в
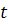 ,
тогда суммарный поток по ,
тогда суммарный поток по
 также является потоком из
также является потоком из
 в в
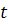 .
Если .
Если
 ,
то поток ,
то поток
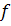 назовем
потоком вдоль путей назовем
потоком вдоль путей
 . .
Предположим, что поток
 продукта продукта
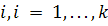 имеет источник
имеет источник
 и
сток и
сток
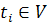 .
Если .
Если
 —
потоки —
потоки
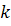 продуктов,
то продуктов,
то
 называется
многопродуктовым потоком в называется
многопродуктовым потоком в
 . .
Входные данные задачи о
максимальном многопродуктовом потоке состоят из ориентированной сети
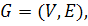 где где
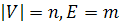 ,
функции ,
функции
 ,
задающей пропускные способности дуг, и значений ,
задающей пропускные способности дуг, и значений
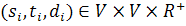 задающих
источник, сток и требуемый объем для каждого продукта задающих
источник, сток и требуемый объем для каждого продукта
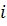 при при
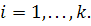 Требуется
максимизировать Требуется
максимизировать
 ,
при условии, что суммарный поток по каждому ребру ,
при условии, что суммарный поток по каждому ребру
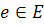 не
превышает не
превышает
 и и
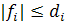 , ,
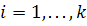 . .
Невзвешенная задача о
максимальном многопродуктовом потоке с ограничением на длину цепей
(LBMCF1) имеет те же входные данные, а также верхнюю границу
 .
Требуется найти максимальный многопродуктовый поток, суммарный поток по
каждой дуге .
Требуется найти максимальный многопродуктовый поток, суммарный поток по
каждой дуге
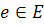 не
превышает не
превышает
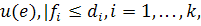 и
поток для каждого продукта является потоком вдоль путей длины не
превышающей и
поток для каждого продукта является потоком вдоль путей длины не
превышающей
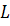 .
Очевидно, задача о максимальном многопродуктовом потоке является частным
случаем LBMCF1, при .
Очевидно, задача о максимальном многопродуктовом потоке является частным
случаем LBMCF1, при
 .
Не ограничивая общности будем считать, что все пары .
Не ограничивая общности будем считать, что все пары
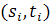 различны,
так как при наличии одинаковых пар различны,
так как при наличии одинаковых пар
 достаточно
просуммировать соответствующие им объемы продукта. достаточно
просуммировать соответствующие им объемы продукта.
Формулировка LBMCF1 в
виде задачи линейного программирования, содержащая
 ограничений
и ограничений
и
 переменных,
может быть построена как задача о многопродуктовом потоке в специально
сконструированной многоуровневой сети [2]. Множество вершин переменных,
может быть построена как задача о многопродуктовом потоке в специально
сконструированной многоуровневой сети [2]. Множество вершин
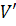 такой
сети содержит копию такой
сети содержит копию
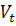 исходного
множества исходного
множества
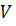 графа графа
 для
каждого дискретного момента времени для
каждого дискретного момента времени
 .
Каждой дуге .
Каждой дуге
 в
исходном графе соответствует дуга в в
исходном графе соответствует дуга в
 из
вершины из
вершины
 уровня уровня
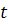 в
вершину в
вершину
 уровня уровня
 .
Кроме того, .
Кроме того,
 содержит
дуги содержит
дуги
 для
всех для
всех
 .
Также на многопродуктовый поток в новой сети накладывается условие, что
для любой исходной дуги .
Также на многопродуктовый поток в новой сети накладывается условие, что
для любой исходной дуги
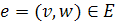 суммарный
поток по всем дугам суммарный
поток по всем дугам
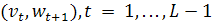 не
превосходит не
превосходит
 .
Для всех .
Для всех
 источник
для продукта источник
для продукта
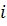 размещается
в вершине размещается
в вершине
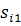 соответствующей
исходной вершине соответствующей
исходной вершине
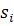 на
уровне на
уровне
 .
Сток располагается в вершине .
Сток располагается в вершине
 соответствующей
исходной вершине соответствующей
исходной вершине
 на
уровне на
уровне
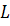 .
Модель ЛП выглядит следующим образом: .
Модель ЛП выглядит следующим образом:
|
![]() Benchmarks Library
Benchmarks Library![]()
Benchmarks Library