![]() Simple
Plant Location Problem
Simple
Plant Location Problem ![]() Benchmarks
Benchmarks ![]()
![]()
Instances
with large duality gap
Allocation of
local optima
Class Gap -C
We get 8465 local optima with respect to the neighborhood Add-Drop-Swap for 9000 random subsets of the set I . On the diagram every sphere corresponds to a local optimum. The sphere radius is number of local optima which situated not far from the distance 10. The minimal radius is 1, the maximal one is 229, average one is 14. Radius of the sphere for the global optimum is 21. The value of objective function for the global optimum is 42145. We get no local optimum with value of objective function less then 45000. The local optimum which has maximal radius 229 has value of the objective function 54081. It locates at distance 16 from the global optimum. There are 134 local optima with sphere radius more then 200. Maximum mutual distance for all pairs of local optima is 41.
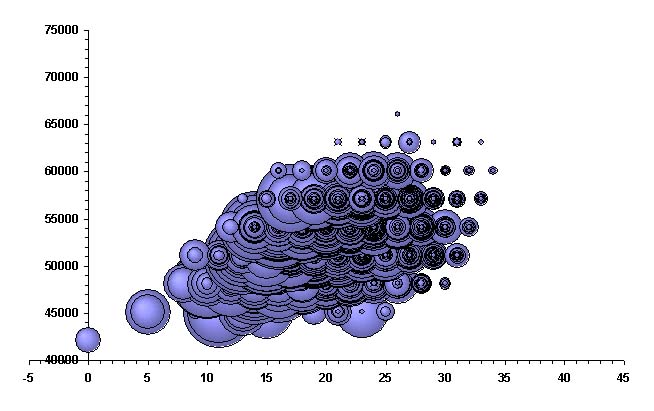
Abscissa axis is Hamming distance to the global optimum.
Axis of ordinates is the value of the objective function.
Instance code is 433.