Дискретные задачи размещения Библиотека тестовых задач

Задача размещения без ограничений на мощности предприятий встречается в литературе под разными названиями:

• задача выбора оптимального ряда изделий одноразового использования [1];

• простейшая задача стандартизации и унификации [2];

• задача оптимизации параметров однородной технической системы [3];

• задача размещения филиалов банка [4];

• задача размещения складов [5];

• задача размещения предприятий [6] и др.

Как и многие математические модели, она допускает различные интерпретации, что оправдывает чисто академический интерес к ее исследованию. При описании модели мы будем следовать наиболее популярной терминологии дискретных задач размещения, хотя другие интерпретации могут быть не менее понятными и наглядными.

Пусть множество I ={1, ..., I} задает перечень возможных пунктов размещения предприятий по производству некоторого однородного продукта. В любом из пунктов iI можно открыть предприятие и величина c_i 0 задает соответствующие затраты. Открытое предприятие может производить продукцию для потребителей в неограниченном количестве.

Перечень потребителей задается множеством J ={1,…, J}. Для каждой пары ij известна величина g_ij0 затрат на производство и доставку продукции потребителю. Задача состоит в том, чтобы найти такое множество открываемых предприятий , которое с минимальными затратами позволяет удовлетворить потребности всех потребителей. С использованием введенных обозначений оптимизационная постановка задачи может быть записана следующим образом:

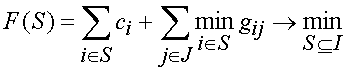
Сформулированная задача является обобщением известной задачи о покрытии множествами [8] и, следовательно, относится к числу NP-трудных в сильном смысле. Для решения простейшей задачи размещения разработаны точные алгоритмы, приближенные алгоритмы с гарантированными оценками точности, Лагранжевы эвристики, вероятностные итерационные алгоритмы локального поиска. Найдены полиномиально разрешимые классы задач. Обзор результатов для данной задачи можно найти, например, в [7].

Литература

1. Береснев В.Л., Гимади Э.Х., Дементьев В.Т. Экстремальные задачи стандартизации. Новосибирск: Наука, 1978.

2. Гимади Э.Х. Выбор оптимальных шкал в одном классе задач типа размещения, унификации и стандартизации. Управляемые системы. Вып. 6 (1970), Новосибирск, Ин-т математики Сиб. отд. АН СССР, с. 57-70.

3. Береснев В.Л. Об одном классе задач оптимизации параметров однородной технической системы. Управляемые системы. Вып. 9 (1971), Новосибирск, Ин-т математики Сиб. отд. АН СССР, с. 65-74.

4. Cornuejols G., Fisher M.L., Nemhauser G.L. Location of bank accounts to optimize float. Management Science. v22 (1977), pp 789-810.

5. Khumawala B.M. An Efficient Branch-Bound Algorithm for the Warehouse Location Problem. Management Science. v18 (1972), pp 718-731.

6. Krarup J., Pruzan P.M. The simple plant location problem: Survey and synthesis. European Journal of Operational Research. v12 (1983),  pp 36-81.

7. Mirchandani P.B., Francis R.L. Discrete Location Theory. John Wiley & Sons, 1990.

8. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М. Мир. 1982.

Главная страница библиотеки