Часть 2. рекурсивно порожденные символьные последовательности: Теоретическое и экспериментальное Исследование

Мы продолжаем изучение взаимосвязи между различными способами порождения символьных последовательностей (с.п.), их сложностью и свойствами языка подслов этих последовательностей [1,2]. Это предполагает исследование комбинаторной сложности с.п. (разнообразия подслов), периодичности с.п., кратности повторений подслов и длины повторов, структуры подслов и т.п. Рассматривается модель сборки с.п. с помощью операций конкатенации и взаимосвязи трудоемкости сборки со сложностными характеристиками с.п. Исследуемые комбинаторные и структурные свойства с.п. мы иллюстрируем примерами на двух последовательностях.

Первая последовательность (ниже Е-п.) была введена А.А. Евдокимовым в связи с решением комбинаторной проблемы «змея в ящике» [1], которая имеет многочисленные приложения. Последовательность порождается простой рекурсивной схемой, но имеет «нерегулярное поведение», которое позволяет длинную цепь в n‑мерном кубе (змею) “хорошо упаковать”. Е-п. является типичным представителем целого семейства с.п. с интересными свойствами [1]. Мы приводим результаты анализа сложностных свойств этой последовательности и различных её числовых характеристик.

Вторая с.п., (её называем с.п. непрерывного кодирования и обозначаем L-п.) имеет отношение к теории дискретных динамических систем и сжатию с.п. кодированием серий, то есть повторений в них букв и подслов. Наш способ порождения этой последовательности близок заданию последовательности слов, которая после выхода известной статьи Дж. Конвея [5] называется в англоязычной литературе “Look and say sequence”[7]. Мы дополняем некоторые известные свойства последовательности слов Конвея и L-п., приводим результаты экспериментального исследования поведения L-п. и формулируем несколько нерешённых вопросов.

Анализировать комбинаторные и сложностные свойства последовательностей нам помогала разработанная ранее программа визуализации с.п. [2,3]. (Программу VIZ см. в http://www.math.nsc.ru/LBRT/k3/Graph/Bruijn.html.) Получаемые с помощью этой программы граф-портреты с.п. позволяют предсказывать различные свойства последовательностей и структуры их подслов, а динамика изменения графов подслов с ростом их размерности характеризует поведение последовательностей “в целом”.

1. Определения

Пусть S = {0,1,¼,m-1} – алфавит из m символов (букв). Слово (последовательность) - это конечная (бесконечная) цепочка, состоящая из букв алфавита S. Множество всех слов в алфавите S, включая пустое слово, обозначаем S^*. Длину слова X обозначаем |X|. Если X и Y –слова, то их конкатенация XY есть результат приписывания слова Y к слову X. Если существуют такие слова X₁ и X₂, что Y= X₁XX₂, то слово X называется подсловом слова Y. Подслово X называется префиксом слова Y, если X₁-пустое слово, и суффиксом, если X₂-пустое слово.

Схемой конкатенации слова X называется такая последовательность слов, в которой каждое слово является либо буквой алфавита, либо конкатенацией двух предшествующих слов из последовательности, причем последовательность заканчивается словом X. Аддитивной сложностью А(X) слова X называется минимальная длина его схемы конкатенации [1].

Отображение j: S^* ® S^* называется морфизмом, если j(XY)=j(X)j(Y) для любых слов X и Y. Действие морфизма j на слово определяется образами букв, то есть j(X)=j(x₁)j(x₂)…j(x_n). Если xÎS, а с.п. X начинается с буквы x, то имеем X = j(X) и с.п. X=X(j,x) называется неподвижной точкой морфизма j. Разнообразие подслов в последовательности (или слове) характеризует функция f(n,X), равная количеству различных слов длины n в X. Она называется комбинаторной сложностью X .

Если существует натуральное k >1, такое что с.п. не содержит подслов X^k для любого XS^* , то говорим, что с.п. является последовательностью ограниченного повторения, или k‑бесповторной.

Графом де Брёйна размерности n называется ориентированный граф = (V,E), где V-множество вершин, E-множество дуг. Множество вершин V = S ⁿ - это все слова длины n в алфавите S. Две вершины a=(a₁,...,a_n) и b=(b₁,..., b_n) соединяются дугой, ориентированной от a к b, если слова a и b перекрываются по n-1 буквам, то есть, справедливы равенства a₂=b₁, a₃=b₂, ... ,a_n=b_n-1. Число вершин в графе равно mⁿ, а число дуг mⁿ⁺¹ . Граф имеет m петель в вершинах, соответствующих словам – константам xⁿ, образованным n-кратным повторением буквы x. Граф связен, однороден и полустепень входа и выхода каждой его вершины равна m.

Последовательность графов i=1,2,... можно определить индукцией по размерности i, поскольку граф является реберным графом для . Последнее свойство легко доказывается по индукции. Оно часто используется при исследовании структуры перекрытия подслов в словах и решении задач комбинаторики символьных последовательностей.

Произвольной с.п. X=x₁,x₂,x₃,... в алфавите S поставим в соответствие путь в графе , который начинается в вершине (x₁,...,x_n ) и последовательно проходит вершины (x_i,...,x_i+n-1) при i=2,3,... Заметаемый этим путем подграф графа называется графом подслов с.п. X. Будем говорить, что он имеет размерность n и обозначать его Gⁿ(X). Таким образом, множеством вершин Vⁿ(X) графа Gⁿ(X) является множество всех подслов длины n в X, а множеством дуг Eⁿ(X) – множество всех подслов длины n+1 в X. По определению

|Eⁿ(X)| - |Vⁿ(X)| = f(n+1,X) - f(n,X) = γ(Gⁿ(X)) - 1,

где γ(Gⁿ(X)) - цикломатическое число графа Gⁿ(X), которое в нашем случае характеризует рост функции комбинаторной сложности с.п.X.

2. Е-последовательность

Эта последовательность определяется в [1] следующей схемой порождения. Пусть

а₁ = 0; b₁ = 1;

a_k+1 = a_k 0 b_k; b_k+1 = a_k 1 b_k; к = 1,2,… (1)

Тогда а₂ = 001, b₂ = 011, а₃= 0010011, b₃ =0011011, а₄ = 0010 01100011011, b₄=0010011.1.0011011 …, и |а_k| = |b_k| = 2^k –1 для любого к.

По определению для слов a_k выполняется свойство префиксной вложимости

a₁ a₂  a₃ a₄ a₅ …,

и потому можно определить бесконечную последовательность Е=lim_n®¥ a_n, префиксами которой являются слова а_k . Эта символическая запись имеет и содержательное толкование. Ведь если слову а_k поставить в соответствие действительное число 0,а_k , то предел последовательности чисел 0,a_k , k =1,2,… и будет числом, соответствующем бесконечной Е-п.

Из схемы рекурсии (1) легко получить следующую конструкцию Е-п.

Пусть (2)

где, - это отрицание слова , а - это слово , прочитанное с конца.

Тогда получим x₂ = 0.0.1, x₃ = 001.0.011, x₄ = 0010011.0.0011011, и из способа задания (2) и схемы (1) легко доказать индукцией по n, что для любого n0 имеем x_n = a_n.

Используя (2) и (1) нетрудно найти формулу для вычисления члена e_i последовательности Е по номеру i . Для этого представим число i в виде i = 2^s (4t +j), где j = 1 или 3, и положим

e_i = 0, если j = 1 и e_i = 1, если j = 3. (3)

Используя (1),(2) и (3), нетрудно установить ряд свойств Е-п.

Свойство 1. Е удовлетворяет схеме Теплица с периодической базовой последовательностью 01(01)……

Действительно, из (3) следует, что e_k = e_2k , и что в Е нечётная подпоследовательность 01(01)… периодична с длиной периода, равным 2.

Свойство 2. Е является непериодической в сильном смысле, поскольку никакое подслово не повторяется в ней подряд 4 раза, то есть Е является 4‑бесповторной.

В [4] доказан более сильный результат - Е содержит подслово X² лишь при | X | = 1, 3 или 5. Найден вид всех таких слов X. Доказательство этого довольно громоздко, и здесь не приводится.

Свойство 3. Е может быть задано действием на буквы 0 и 1 “условного морфизма” следующим образом: применяем подстановку 0 ® 001, 1 ® 011 к буквам, стоящим на нечётных позициях, а тождественную подстановку 0 ® 0 , 1 ® 1 к буквам на чётных позициях. Обозначим это отображение f. Его последовательные степени будут иметь вид: f(0) = 001, f ²(0) = f(001) = 0010011, f ³(0) = f(0010011) = 001001100011011, …. и тогда из (1): а₂ = f (0), а₃ = f ²(0), а₄ = f ³(0), …

Используя (3) и свойство 1, легко показать, что а_n = f ⁿ(0) для любого n, и, следовательно, Е = f ^¥(0) = lim _n®¥ f ⁿ(0).

Заметим, что хотя в нашей конструкции Е определяется действием “двойного” морфизма f, но можно показать, что Е не является неподвижной точкой никакого “одинарного” морфизма, или, более точно, j(Е)Е ни для какого морфизма j.

Свойство 4. Функция А (а_n) аддитивной сложности слова f ⁿ(0) = а_n растёт линейно по n, т.е. имеет с точностью до порядка величины логарифмический рост от длины слова |fⁿ(0)| = |a_n| = 2ⁿ -1 . Более точно, для аддитивной сложности Е-п. при n6 справедливы неравенства

3 n – 2 А (а_n) 4 n – 6,

где верхняя оценка получается с помощью алгоритма сборки, основанного на схеме (1), и схемах сборки а_n для начальных значений n.

Свойство 5. Графы подслов Gⁿ(Е) при n7 разбиваются на два класса гомеоморфных графов в зависимости от значения их размерности n. Эти графы имеют следующий вид.

Графы Gⁿ(Е) первого класса со значениями размерности, равными n=2^k –1, при k3, изображены на рис.1.

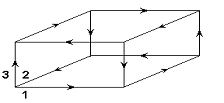
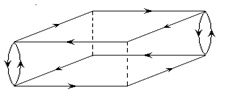
Рис.1 Рис. 2

Графы G ⁿ(Е) второго класса размерности n2^k –1, при k3, изображены на рис.2. Вид графов G ⁿ(Е) при n6 устанавливается непосредственно, или это легко сделать с помощью программы VIZ (см. ниже).

Свойство 6. При n7, С(n,E) = 4 n.

Как было сказано выше, для функции комбинаторной сложности любой последовательности X справедливо С(n,X) = |V ⁿ(X)| , то есть для нахождения С(n,E) достаточно знать функцию роста числа вершин в графах подслов Gⁿ(Е). По свойству 5 достаточно произвести подсчёт для двух графов на рисунках 1 и 2, которые представляют классы гомеоморфных графов. Это легко сделать, используя вид этих графов [6].

Последнее хорошо иллюстрирует, как для распознавания свойств с.п. помогает специально разработанная нами технология визуализации графов подслов на графах де Брёйна. Этот программный инструментарий позволяет легко и быстро идентифицировать с.п. с различными способами их порождения, находить повторы подслов и кратность их вхождения, вычислять различные сложностные характеристики с.п. (применение к анализу генетических текстов подробнее см. в [2], о программе VIZ см.[3,4]).

3. Последовательность непрерывного кодирования

Пусть в алфавите S задано базовое кодируемое слово W₀ длины |W₀|. Кодируемое слово разделяется на подслова – серии, состоящие из последовательных одинаковых букв, (соседние серии состоят из разных букв). Серию xx…x записываем в виде x^d, где d – число букв x в этой серии. Например:

S ={1,2,3} и W₀ = 11 2 11 22 1 22 11 222 1 3 2 = 1² 2¹ 1² 2² 1¹ 2² 1² 2³ 1¹ 3¹ 2¹

Определим оператор кодирования S(V) слова V. Каждая серия s=x^d слова V кодируется кодовой парой S(x^d)=dx, в которой на первом месте буква, обозначающая длину этой серии, а вторая совпадает с буквой кодируемой серии. Кодовые пары записываются в том же порядке, как расположены кодируемые серии. Последовательность кодовых пар для последовательности серий кодируемого слова образует кодовое слово. В нашем примере:

S(W₀)=S(11 2 11 22 1 22 11 222 1 3 2)=1,12,21,22,11,22,21,32,11,13,12

Для выделения кодовых пар и серий, мы разделяем кодовые пары запятой, а серии пробелом. Обратную процедуру однозначного восстановления слова по кодовому слову называем декодированием. Оператор декодирования обозначаем через S^-1.

Определим процедуру построения бесконечной последовательности.

Возьмем базовое слово W₀ =11 и по нему построим кодовое слово W₁ = S(W₀), которое считаем началом W₁ последовательности L(W₀). Затем, начиная с первой серии слова W₁, оператором S последовательно кодируем серии слова W₁. Каждую вновь полученную кодовую пару приписываем к концу построенного слова. Получаем слово со следующим номером, и т.д. Так, если серия с номером k в слове W_k есть s_k= x^d, то

W_k+1= W_k•S(s_k)= W_k •dx

Запишем несколько первых шагов этого кодирования, а справа для сравнения запишем шаги построения слов Конвея [5].

Непрерывное кодирование Слова Конвея

W₀= 11, 11

W₁= 21, s₁ = 2, 21

W₂= W₁•S(s₁)= 21,12 s₂ = 11, 12,11

W₃= W₂•S(s₂)= 2112,21 s₃ = 22, 11,12,21

W₄= W₃•S(s₃)= 211221,22 s₄ = 1, 31,22,11

W₅= W₄•S(s₄)= 21122122,11 s₅ = 22, 13,11,22,21

W₆= W₅•S(s₅)= 2112212211,22 s₆ = 11, 11,13,21,32,11

W₇= W₆•S(s₆)= 211221221122,21 s₇ = 222, 31,13,12,11,13,12,21

W₈= W₇•S(s₇)= 21122122112221,32 s₈ = 1, 13,21,13,11,12,11,13,12,21

W₉= W₈•S(s₈)= 2112212211222132,11 s₉ = 3, 11,13,12,21,13,31,12,31,13,11,22,11

……… ………

По построению  W_i  является префиксом для W_i+1 при i ≥ 1 и, тем самым, определена последовательность L= lim_i®¥ W_i , которую называем последовательностью непрерывного кодирования и обозначаем L-п. Позиции букв последовательности нумеруем, начиная с 1. Кодовые пары и кодовые слова в последовательности начинаются с нечетной позиции. Когда мы рассматриваем последовательность вместе с базовым словом, то позиции букв в базовом слове нумеруем числами £ 0.

Пусть V – произвольное слово. Кодовое слово W=S(V), полученное в результате кодирования слова V назовем потомком слова V, а слово V– предком слова W. Сформулируем некоторые простые свойства L-п.

Свойство 1: В L-п отсутствуют кодовые слова вида xyzy при любых x, y, z, так как соседние кодовые пары кодируют серии из различающихся букв. Другими словами, соседние четные позиции содержат разные буквы.

Свойство 2: Операция декодирования однозначно восстанавливает предка для любого кодового подслова из L-п.

Свойство 3: Длина любой серии в L-п не превышает 3.

Действительно, пусть серия длины 4 является подсловом в L-п. Каждое подслово длины 4 содержит пару букв на двух чётных позициях. Но по свойству 1 эти буквы должны быть различными, значит, подслово длины 4 не может быть серией или её частью.

Свойство 4: Любая серия длины 3 начинается с начала кодовой пары, т.е. в нечетной позиции (иначе серия содержит одинаковые буквы в двух соседних четных позициях, которые по свойству 1 должны быть различными).

Свойство 5: L-п не содержит подслова 3x3 для любого x. Действительно, кодовое слово y3x3 недопустимо по свойству 1. Кодовое слово 3x3y недопустимо как кодовое слово для двух соседних серий длины 3, из которых одна начинается в четной позиции, что противоречит свойству 4.

Свойство 6. Если A–подслово четной длины в L-п, то |S(A)| ³ |A|.

Доказательство. Пусть A – подслово четной длины в L-п. По определению оператора кодирования потомок любого слова содержит столько кодовых пар, сколько серий содержит кодируемое слово. Если подслово A является кодовым словом, то по свойству 1 в нем на соседних четных позициях находятся разные буквы, а значит, они не могут входить в одну серию. Если же слово A не является кодовым словом, то при некотором xÎS все его нечетные позиции содержат буквы из четных позиций кодового слова xA и, следовательно, не могут входить в одну серию. Таким образом, в обоих случаях количество кодовых пар в кодовом слове не меньше чем количество пар букв в его предке A.

Свойство 7. Последовательность непрерывного кодирования является непериодической.

4. Эксперименты с последовательностью.

Для анализа свойств последовательностей, порождаемых описанным алгоритмом, были проведены вычислительные эксперименты. Генерировались последовательности до 2•10⁹ букв при разных базовых словах. Для построенных последовательностей вычислялись различные числовые характеристики. Последовательность разбивалась на отрезки длиной 10⁵ букв, и числовые характеристики вычислялись независимо для каждого отрезка. Исследовалось изменение числовых характеристик на отрезках разбиения и поведение этих характеристик на всей последовательности.

Были вычислены частоты встречаемости букв в отрезках и динамика изменения частот с ростом длины последовательности. Оценивался рост функции комбинаторной сложности. Оказалось, что для значений n>30 функция комбинаторной сложности мажорируется линейной функцией с коэффициентом, приблизительно равным 200, причем этот эффект наблюдался при выборе различных базовых слов. Результаты вычислений показали, что поведение характеристик с ростом длины последовательности качественно слабо зависит от выбора различных слов в качестве базовых.

Выполнен анализ поведения последовательности при различных базовых словах. Поставлен ряд численных экспериментов для определения количественных характеристик последовательности. Вычисления проводились на последовательностях различной длины – от 400 000 000 до 1 200 000 000 символов, а также для 67-ого слова последовательности слов Конвея[5] (длина которого около 250 000 000 символов).

5. Результаты вычислений

1) Зависимость количества различных подслов в последовательности от длины подслова.

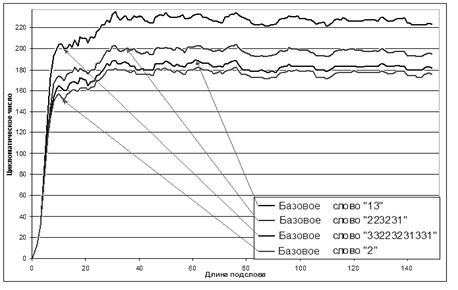
Рисунок 1. График зависимости цикломатического числа L-последовательности от длины подслова при различных базовых словах.

Зависимость количества различных подслов в последовательности от длины подслова является нелинейной, т.е. прирост непостоянен. Расчёты проводились непосредственным построением дерева подслов. Данный вывод был сделан исходя из результатов построения дерева подслов последовательностей при различных базовых словах и на последовательностях различной длины (до 500 000 000 символов).

Как видно из рисунка 1, поведение цикломатического числа слабо зависит от базового слова, меняется лишь его значение. Также видно, что для подслов малой длины, цикломатическое число быстро возрастает и устанавливается на определённом уровне, после чего происходят колебания цикломатического числа в диапазоне 10-12 слов.

2) Доли символов в последовательности L-п.

Было подсчитано количество единиц, двоек и троек, и их долевое содержание в последовательности L-п. Исходя из полученных результатов, можно сказать, насколько часто встречаются серии длины 1, 2 и 3. График доли содержания единиц (на логарифмической шкале) представлен на рисунке 2. Графики доли двоек и троек ведут себя аналогично.

Как видно из графиков, на первых шагах построения (примерно первые 20 000 000 символов), последовательность ведёт себя неустойчиво, однако далее колебания коэффициентов становятся всё меньше и меньше, стремясь при этом к определенным числам. Таким образом, доля единиц на последовательности длины n составляет примерно 49,5% от общего числа символов. Доля двоек и троек – 32,04% и 18,46% соответственно.

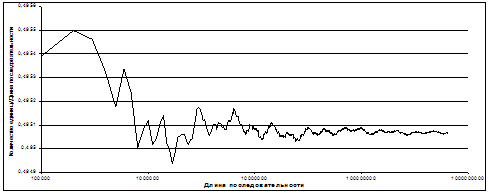
Рисунок 2. Доля единиц в последовательности L-п.

3) Отношение номеров позиций порождающего и порождаемого символов.

При порождении последовательности L-п серия букв начиная с позиции i (порождающий символ) кодируется кодовой парой, которая помещается в позицию j (порожденный символ). Далее было проведено исследование скорости роста последовательности – на сколько позиций отстаёт номер позиции порождающего символа от номера позиции порождаемого.

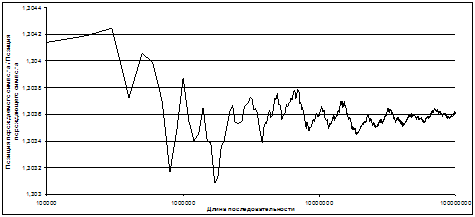
Рисунок 3. Зависимость позиции порождённого от позиции порождающего символов в L-п.

Были построены графики этих зависимостей (рисунок 3). Как видно из графика, с увеличением длины последовательности, отношение номеров позиций порождающего и порождаемого символов примерно равно 1,3 и стремится к константе Конвея С~1,303 [5].

Можем сделать вывод, что данная зависимость описывается функцией вида y = const·С^x, где величина const зависит от базового слова, а С– константа Конвея.

4) Длина последовательности, необходимая для выявления всех возможных подслов фиксированной длины.

Для ответа на вопрос: какой длины последовательность нужно построить, чтобы в ней встретились все подслова заданной длины, содержащиеся в бесконечной последовательности, были проанализированы следующие характеристики. Для слов длины от 1 до 420, была вычислена первая позиция последнего из различных подслов, встречающихся в данной последовательности, и расстояние до предпоследнего подслова (рисунки 4 и 5).Исходя из этих графиков, мы можем оценить длину необходимой последовательности.

Оказалось, что поведение этих функций не зависит от выбора базового слова последовательности.

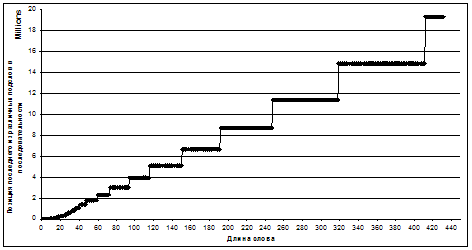
Рисунок 4. Зависимость первой позиции последнего из различных подслов найденных в последовательности L-п от длины подслова.

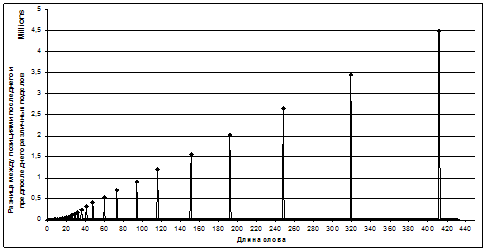
Рисунок 5. Зависимость величины промежутка между позициями появления последнего и предпоследнего подслова фиксированной длины в L-п.

Полученные экспериментальные результаты позволяют сделать следующие выводы о свойствах последовательности L-п и о последовательностях с другими начальными словами:

1. поведения характеристик не зависит от выбора начального слова;

2. поведение функции цикломатического числа:

a. при малых значениях (от 1 до 10) цикломатическое число быстро возрастает;

b. в диапазоне 10-30 цикломатическое число увеличивается почти линейно, но с колебаниями;

c. далее, колебания происходят вокруг некоторой константы, причём константа разная при разных базовых словах, а колебания нерегулярные;

3. кривая, отображающая номер первой позиции последнего из различных подслов фиксированной длины найденных в последовательности в зависимости от длины подслова:

a. длина начального отрезка последовательности в котором обнаруживаются все её слова фиксированной длины экспоненциально растет от длины слова;

b. рост длины необходимого отрезка происходит при специальных длинах слова.

Литература

1. Евдокимов А.А. Анализ, сложность и реконструкция символьных последовательностей. // Вестник ТГУ, 2005, N 14, С. 4-12.

2. Евдокимов А.А., Левин А.А. Графические модели и комбинаторика генетических и математических символьных последовательностей // Вычислительные технологии. Новосибирск. 2002, Том 7, С. 274-278.

3. Евдокимов А.А., Левин А.А. Методы визуализации графов подслов символьных последовательностей // Вычислительные технологии. Специальный выпуск трудов международной конференции "Вычислительные и информационные технологии в науке, технике и образовании". Часть II. 2003. Т. 8. С. 5-11.

4. Демонстрация последовательностей на графах де Брейна http://www.math.nsc.ru/LBRT/k3/Graph/Bruijn.html

5. Conway, J. H. "The Weird and Wonderful Chemistry of Audioactive Decay." Open Problems in Communications and Computation.(Ed . T. M. Cover and B. Gopinath). New York: Springer-Verlag, pp. 173-188, 1987.

6. Смолина Ю.В. Дипломная работа ММФ НГУ, 2002г.

7. http://mathworld.wolfram.com/LookandSaySequence.html