ИМ СО РАН
![]() Лаб."Математические модели принятия решений"
Лаб."Математические модели принятия решений"
Прикладные проекты
|
Задача управление автоматизированным складом комплектации заказов Заказчик: Huawei Noah’s Ark Lab, Китай, 2020-2021 Построена математическая модель для зачади управления автоматизированным складом комплектации заказов. Разработан алгоритм поиска с чередующимися окрестностями на пространстве перестановок и конструктивная эвристика для построения эффективного расписания по заданной перестановке. Алгоритм реализован на С++. Постановка задачи: рассматривается процесс сборки и упаковки заказов на крупном автоматизированном складе компании. Заказы обрабатываются на нескольких параллельно работающих производственных линиях, каждая из которых оснащена параллельно работающими станками на обеих стадиях обработки заказов (сборки и упаковки) и промежуточным буфером. На стадии сборки задействован ограниченный парк автоматических транспортных роботов. Роботы доставляют паллеты с необходимым товаром со склада на станции сборки, а затем возвращают паллеты на склад. Максимальное время сборки заказа ограниченно и не может превышать заданного порога. Требуется найти расписание, позволяющее минимизировать суммарное время обработки всех заказов. Для решения задачи разработан алгоритм поиска с чередующимися окрестностями на пространстве перестановок и конструктивная эвристика для построения эффективного расписания по заданной перестановке. Алгоритм реализован на С++. Проведены тесты на реальных данных. За короткое время (до 20 минут на персональном компьютере) алгоритму удается находить решения с погрешностью не более 5% на примерах с 2000 заказов. |
|
|
Задача минимизации числа серверов для обслуживания виртуальных машин на заданном горизонте планирования Заказчик: Компания Huawei 2021 |
||
|
|
Для задачи распределение виртуальных машин по серверам c NUMA архитектурой получены нижние и верхние оценки числа требуемых серверов. Разработан оптимизационный алгоритм, основанный на идеях метода генерации столбцов. Алгоритм продемонстрировал малое отклонение от оптимальных решений и высокую скорость выполнения на тестовых примерах заказчика. Постановка задачи: Серверы в дата-центре имеют одинаковую архитектуру (см рис.). Каждый сервер разделен на два NUMA-узла, в каждом из которых имеется одинаковое количество ядер и оперативной памяти. Каждая виртуальная машина требует определенное число ядер и оперативной памяти, например, 1 ядро и 1 Гб. RAM (маленькая ВМ) или 32 ядра и 64 Гб. RAM (большая ВМ). Множество виртуальных машин разбивается на два непересекающихся подмножества: маленькие виртуальные машины и большие. Маленькая виртуальная машина должна быть помещена на один из узлов сервера, тогда как большая машина делится на две равные части, и обе помещаются на соответствующие им узлы. Миграция виртуальных машин с сервера на сервер или с узла на узел на одном сервере запрещена. Для каждой виртуальной машины известно время ее создания и время окончания работы. Требуется определить минимальное число серверов для размещения всех виртуальных машин и их распределение по серверам с учетом NUMA-архитектуры. Премия за проект от компании Huawei |
|
|
Выбор оптимального маршрута движения сельскохозяйственной техники по полю Заказчик ООО "РусАгро" 2021 |
||
|
Разработан алгоритм, вычисляющий время необходимое для обработки поля конкретной единицей техники, при заданной схеме движения и заданном направлении линии сева. Создана система определяющая генеральную линию сева и схему движения для заданной техники. Постановка задачи: Рассматривается задача определения оптимального маршрута движения сельскохозяйственной техники по полю. Для каждого поля необходимо выбрать генеральную линию сева. Остальные работы будут проходить либо параллельно линии сева (сев, обработка ХСЗР и уборка), либо под заданным углом (зяблевая обработка почвы). Необходимо так выбрать генеральное направление, чтобы время, потраченное на выполнение всех работ на поле, было минимальным. Известно несколько возможных вариантов схем движения техники по полю при заданном направлении: |
||
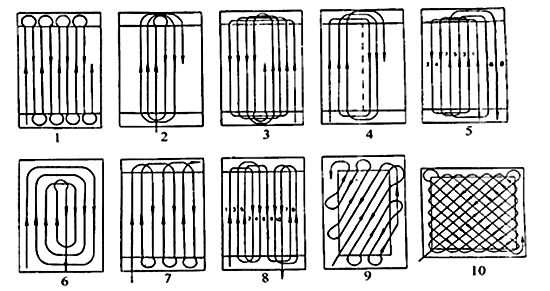 |
1 – челночный; 2 – всвал; 3 – вразвал; 4 – перекрытием; 5 – комбинированный; 6 – круговой; 7 – челночный односторонний; 8 – пропашка; 9 – диагонально-челночный; 9 – диагонально-челночный;
|
 |
| Время движения для каждой схемы складывается из времени движения по прямой (с постоянной скоростью) и времени, затрачиваемом на поворот. Поворот является самой сложной составляющей при работе на поле. Для осуществления поворотов изначально поле вспахивается по периметру (происходит обсев поля) и затем сев идет не до края поля, а до обсева. Необходимая площадь, требуемая для разворота (например, в схеме 1) больше, чем площадь для поворота на 90° (например, в схемах 2,3,4,5,8), поэтому при выборе движения по схеме 1 необходимо изначально выполнить 3 круга обсева, а для других схем 2. | ||
|
Алгоритмы оптимизации маршрутов поставок и выбора типов установок подготовки газа Заказчик: ООО «Газпромнефть НТЦ» 2020 Исследована задача оптимизации маршрутов поставок и выбора типов установок подготовки газа с целью минимизации расходов на прокладку трубопроводов и строительства установок. Разработан алгоритм решения задачи поиска оптимальной конфигурации оборудования, подготовки и транспортировки газа для группы месторождений. Постановка задачи: Имеется множество месторождений (скважин) и несколько пунктов сдачи газа в магистральный трубопровод. На каждом из месторождений производится добыча газа и осуществляется его предварительная или комплексная подготовка (с помощью установок предварительной или комплексной подготовки газа). При комплексной подготовке газ обрабатывается до состояния сухого очищенного газа. Далее он отправляется по трубопроводу в пункт сдачи напрямую, либо транзитом через одно или несколько месторождений. При предварительной подготовке газ по мультифазному трубопроводу направляется сначала для комплексной подготовки напрямую или транзитом на пункт комплексной подготовки, после чего уже сухой очищенный газ отправляется в пункт сдачи напрямую или транзитом. Известны цены и диаметры труб. Между каждой парой месторождений можно проложить трубопровод только одного типа: для сухого очищенного газа или газа после предварительной подготовки. Весь добытый газ должен быть подготовлен и доставлен в пункт сдачи газа. Задача состоит в построении системы трубопроводов и выбора установок подготовки газа, чтобы минимизировать суммарные расходы по доставке газа со всех месторождений в магистральный трубопровод.
|
 |
|
|
|
|
Задача оперативного управления складом Заказчик: RLT, Ravago Logistics Terneuzen, Netherlands 2019 г. Построена математическая модель для задачи оперативного управления складом. Модель использует правило FIFO (first in – first out). Разработан генетический алгоритм с использованием мультиагентной системы и реализован на С++. Результаты работы сравниваются с результатами получаемыми с помощью модели FIFO. Постановка задачи: Рассматривается здание с несколькими складами. Для склада задано количество товара каждого вида и его расположение по комнатам. Предполагается, что в каждой комнате может храниться товар только одного вида. Каждый склад имеет одни ворота для обслуживания грузовиков и один ворота для разгрузки товара из центральной зоны. В каждый момент времени склад может обслуживаться только через одни ворота. Предполагается, что имеется достаточное количество погрузчиков для обслуживания всех грузовиков и центральной зоны. Время погрузки одного поддона не зависит от вида товара или от местонахождения на складе. Центральная зона является производственной линией, которая в каждый момент производит не больше двух видов товара. |
 |
| Произведённый товар необходимо поместить на склад во всём объёме сразу после производства. Расписание работы центральной зоны считается известным на весь день. Рассматриваются грузовики двух типов – привозящие и увозящие товар.Считается известным время прибытия каждого грузовика, количество и вид товара. Запрещается прерывание обслуживания. Для решения задачи требуется найти распределение грузовиков и центральной зоны между складами и указать время начала обслуживания для каждого из них таким образом, чтобы суммарное время ожидания грузовиков было минимальным.Алгоритм запрограммирован на языке С++. Тесты проводились на примерах с 6 складами, 18 видами товаров и 90 грузовиками (включая виртуальные), что соответствует одному рабочему дню. Количество комнат на каждом складе – 64. Вместимость грузовиков варьируется от 10 до 19 единиц груза. Грузовики начинают прибывать с 6:00, позднее возможное время прибытия последнего грузовика – 22:00. Данные генерировались близкими к реальным, учитывалась частота востребованности того или иного вида груза и среднее количество прибывающих грузовиков в час. Решение, выдаваемое алгоритмом, представляет распределение грузовиков между складами и расписание на каждом складе, имеющее наименьшее значение целевой функции. | |
Задача маршрутизации транспортных средств с многократным посещением клиентов Заказчик: ООО «Магнат Трейд Энтерпрайз», Екатеринбург, 2018 |
|
|
Для задачи построения маршрутов для транспортных средств на конечном временном интервале построена модель частично-целочисленного линейного программирования. Разработан метод локального поиска с чередующимися окрестностями, усиленный методом поиска с запретами. Постановка задачи: Компания, обслуживающая клиентов, имеет множество транспортных средств ограниченной грузоподъёмности, находящихся в разных депо. Известно множество клиентов. Каждый клиент имеет свою частоту посещения и обслуживается одним и тем же транспортным средством. Частота посещения задаётся на весь плановый период, при этом интервалы между посещениями должны быть одинаковыми (раз в неделю по понедельникам, раз в две недели, и т. п.). Время посещения может быть любым в рамках рабочей смены, т. е. порядок посещения клиентов внутри рабочего дня может быть произвольным. Требуется построить такие маршруты посещения всех клиентов, чтобы суммарное пройденное расстояние было минимальным, а рабочее время водителей укладывалось в рабочую смену. Для решения поставленной задачи построена модель частично-целочисленного линейного программирования и разработан гибридный алгоритм локального поиска с чередующимися окрестностям, использующий метод штрафов для расширения области поиска. Алгоритм способен решать примеры большой размерности за сравнительно небольшое время на персональном компьютере. Для повышения эффективности алгоритма применяются вероятностные окрестности, а также процедуры интенсификации и диверсификации поиска. Алгоритм реализован на языке C++ с использованием компилятора MSVC++ 14.16 со стандартными release параметрами. Данные для тестирования алгоритма были предоставлены российской логистической компанинадо посещать два раза, а остальные клиенты должны посещаться четыре раза. Имеется три депо, расположенных на расстоянии около 250 км друг от друга.
|
 |
Оптимизация производства тротуарной плитки Заказчик: ООО «Выбор» Новороссийск, 2017 г. |
|
 |
Получена новая математическая модель и разработан стохастический метод локального поиска с запретами для оптимизации расписаний производства тротуарной плитки методом полусухого вибропрессования. Модель учитывает технологические задержки при переходе от одного типа продукции к другому, минимальные партии производства, разнородность заказов клиентов и наличие запасов на складе. В качестве критериев оптимизации выступает штраф за опоздание заказов относительно директивных сроков и суммарная стоимость хранения готовой продукции на складе. Постановка задачи: Имеется станок, предназначенный для производства разнотипной продукции. Для каждого типа известна производительность станка, т.е. количество продукции за час работы и минимально допустимая партия, меньше которой нельзя производить из-за технологических особенностей производства. При переходе от одного типа продукции к другому, требуется переналадка оборудования. Длительность переналадки зависит от обоих типов и может быть различной для разных пар. Для хранения готовой продукции имеется склад неограниченной вместимости. Известна удельная стоимость хранения продукции. Предполагается, что в начальный момент времени на складе имеется определенный запас продукции каждого типа. Клиенты делают заказы на производство продукции. По каждому заказу задан директивный срок его выполнения и объемы партий продукции различного типа. При выполнении заказа продукция либо берется со склада, полностью или частично, либо производится в объеме не меньше минимально допустимой партии и отправляется на склад. Заказ считается выполненным, когда вся заказанная клиентом продукция оказалась на складе. Если этот момент позже директивного срока, то выплачивается штраф за задержку заказа. Штраф прямо пропорционален длительности задержки. Требуется найти такое расписание работы станка, чтобы минимизировать суммарный штраф за возможные задержки заказов и суммарную плату за хранение готовой продукции на складе. |
Задача закупки и экспорта лома черных металлов Заказчик: ДВФУ, Владивосток, 2017 г. |
|
|
Построена математическая модель в терминах линейно-целочисленного программирования для задачи оптимизации деятельности предприятия скупки–продажи лома черных металлов. Проведены расчеты на данных, предоставленных одной из логистических компаний г. Владивосток. Постановка задачи: Предприятие занимается скупкой лома черных металлов и затем экспортирует его по морю на судах разной вместимости. На плановый период известен спрос на лом и предприятие, в рамках своих мощностей, стремится оптимально организовать свою деятельность для максимизации прибыли. Лом черных металлов делится на разные категории и закупается предприятием у региональных поставщиков. На плановый период известны объемы предложения лома каждой категории у каждого из поставщиков. Закупочная цена на лом зависит от общего объема приобретаемого компанией лома за плановый период. Приобретенный лом хранится на складе предприятия. Вместимость склада достаточно велика чтобы не ограничивать объемы закупки, но хранение металлолома сопровождается издержками предприятия. В день на склад может быть выгружено не более определенного количества лома. На складе лом взвешивается, вычитается стандартный процент на технический засор, в результате чего определяется, сколько из всего привезенного объема лома принадлежит той или иной категории. После взвешивания происходит расчет с поставщиками. |
 |
|
От поставщиков на склад лом
доставляется собственным грузовым автомобилем предприятия со штатным
водителем и, при необходимости, арендованным автотранспортом разной
грузоподъемности. Известна стоимость аренды каждого
автомобиля.
Экспорт лома осуществляется морским путем судами разной вместимости. Склад компании находится в портовой зоне, поэтому предприятие не несет транспортных издержек при доставке металлолома со склада на транспортировочное судно. На экспорт идет лом только одной категории, и предприятие несет издержки на переработку лома в эту категорию. На складе хранится лом только экспортируемой категории. Стоимость продаж лома в плановом периоде фиксирована. Отправка груза за рубеж сопровождается издержками на оформление необходимых документов и оплатой фрахта за каждую отгруженную единицу лома. На экспорт в день может быть отгружено не более одного судна. На плановый период требуется – определить объемы закупки лома рассматриваемых категорий, – организовать доставку лома автотранспортом от поставщиков на склад предприятия, –установить когда, в каком объеме и каким судном экспортировать лом так, чтобы максимизировать прибыль предприятия на плановый период.
|
|
Оптимизация работы гравитационного накопителя электроэнергии Заказчик: ООО «Энергозапас», Новосибирск, 2017 |
|
 |
Разработан алгоритм оптимизации работы гравитационного накопителя электроэнергии, позволяющий максимизировать коэффициент его полезного действия. Постановка задачи: Гравитационный накопитель электроэнергии предназначен для хранения и последующей генерации электроэнергии с помощью, так называемых энергетических ячеек. Каждая ячейка состоит из шахт, в которых поднимаются и опускаются грузы, а электрическая энергия преобразуется таким способом в потенциальную энергию грузов. Конструкция накопителя · базируется на регулярно расположенных вертикальных несущих колоннах; · соседние колонны связаны сверху горизонтальными рамами; · рамы накрывают вертикальные шахты с направляющими для перемещения грузов, также предусматриваются технологические шахты без грузов; · грузы перемещаются в шахтах вертикально из верхнего положения в нижнее и наоборот; · груз в верхнем положении через раму передает нагрузку на колонны; · грузы перемещаются с помощью подъемно-транспортного механизма, который состоит из одного асинхронного двигателя, двух кареток снабженных механизмами зацепов грузов и полиспастом, гибкого плоского каната, передающего тяговое усилие от двигателя через каретки к грузам, натяжителей троса на двух его концах; · каретки перемещаются вертикально в шахтах, а в верхнем положении они могут перемещаться и горизонтально - между шахтами; · вертикальное перемещение кареток происходит «по принципу коромысла»: сумма вертикальных координат кареток постоянна, если одна каретка движется вверх, то другая вниз; · каретки могут перемещаться горизонтально между шахтами только в верхнем положении, горизонтальные траектории кареток пересекают различные рамы; \ · двигатель расположен в центре подъемно-транспортного механизма, а каретки справа и слева от двигателя, под двигателем груза нет; · двигатель, и связанные с ним трос, каретки, шахты в зоне доступности кареток и грузы в шахтах объединяются в функциональную единицу накопителя – энергетическую ячейку, все энергетические ячейки накопителя одинаковые; · совокупность регулярно расположенных энергетических ячеек определяет конструкцию накопителя в целом. |
|
Наглядное представление о накопителе можно получить из рисунка. На нем изображен вид сверху на регулярную структуру накопителя. Синие квадраты и кружки в них – это схематическое обозначения шахт и грузов. Коричневые квадратики в углах – это несущие вертикальные колонны. Энергетические ячейки направлены сверху вниз и обслуживаются двигателями, расположенными на одной (зеленой) линии. Последняя шахта энергетической ячейки с необходимостью пустая, чем и обеспечивается возможность положения: все грузы вверху. Кроме этого, предусматривается еще технологические шахты для натяжителей троса. На стыке двух энергетических ячеек достаточно одной такой шахты, в которой разместятся оба натяжителя. На рисунке изображен вариант стыковки двух множеств энергетических секций на 150 шахт, секции вытянуты сверху вниз. Конструкционные ограничения работы накопителя · сумма вертикальных координат кареток одной энергетической ячейки постоянна, если одна из кареток находится в верхнем положении, то связанная с ней каретка располагается внизу; · при вертикальном движении кареток обязательно, одна и только одна каретка движется с грузом; · в пределах одной рамы в фиксированный момент времени может двигаться только один груз, и не больше; · не во всех шахтах перемещаются грузы, некоторые из шахт зарезервированы под технологические нужды; · в случае ремонта одной энергетической ячейки отключаются и соседние ячейки, здесь соседство определяется по пересечениям одних и тех же рам; · при ремонте груза из конструкции накопителя исключается вся рама, в которой расположен груз, и выключаются все ячейки, пересекающие эту раму; · исключение из конструкции накопителя отдельных ячеек носит локальный характер, можно сказать, что мы всегда находимся «в окрестности» полностью работающего накопителя. Система команд накопителя |
 |
|
· Под расписанием работы накопителя энергии понимаем последовательность команд, управляющих накопителем; · управление накопителем в целом разбивается на согласованное управление энергетическими ячейками; · каждая энергетическая ячейка воспринимает команду для каретки в нижнем положении; · для нижней каретки указывается номер шахты/груза куда она должна переместиться, дополнительно указывается момент времени, когда следует начинать выполнение команды на перемещение нижней каретки; · команда перемещения выполняется за два такта: каретка сначала поднимается вверх, а затем, уже в верхнем положении, каретка перемещается от текущей шахты к шахте с заданным номером; · выполнение данной команды автоматически означает, что связанная каретка движется вниз в той шахте, над которой она находилась до выполнения команды; · до выполнения команды следует определить, поднимать груз, или оставить его внизу; · если в шахте под верхней кареткой до выполнения команды груз располагается вверху, то верхняя каретка опускает груз, а нижняя поднимается без груза, в противном случае нижняя каретка поднимает груз; · длительность выполнения команды перемещения нижней каретки известна заранее и задается в виде матрицы в двух вариантах, один из них содержит время движения с грузом, а второй – без груза; · в длительности выполнения команды содержится интервал, когда двигатель разогнан до рабочих оборотов и только тогда происходит генерация энергии в сеть и потребление мощности из сети. Наличие такого интервала объясняется двумя причинами: генерация/потребление отсутствует во время горизонтального движения каретки, в связи с инерцией грузов и ротора двигателя требуется небольшое время для выхода на рабочие характеристики (для разгона), этот разгон условно занимает 1 секунду, плюс одна секунда на торможение на заключительной стадии вертикального движения груза. Требуется разработать алгоритм, который для заданного графика мощности потребления/генерации энергии составляет непротиворечивое расписание работы механизмов накопителя энергии, удовлетворяющее требованиям безопасности и оптимальное в смысле КПД. |
|
Задача оптимизации автопарка и маршрутов транспортных средств Заказчик: ООО «Чистая вода», Новосибирск, 2015 г. |
|
|
Построена математическая модель для задачи оптимизации автопарка и маршрутов транспортных средств. Разработан алгоритм сокращающий число привлекаемых транспортных средств и длину общего пройденного расстояния. Постановка задачи: Задано конечное множество клиентов и склад продукции, где базируются транспортные средства. Каждый клиент имеет временное окно, в котором должно начаться и закончиться его обслуживание. Известна длительность обслуживания и объем доставляемого груза. Транспортные средства (ТС) имеют различную грузоподъемность. За каждым ТС закреплен водитель, который работает в определенную рабочую смену, например, с 7:00 до 16:00 или с 13:00 до 23:00. В ходе работы водитель обязан делать перерывы на отдых. Для перерывов заданы длительность и временные окна. Требуется построить маршруты для ТС и доставить грузы всем клиентам так, чтобы суммарные затраты на привлеченный автопарк и перевозку были бы минимальными. Для указанной задачи построена модель целочисленного линейного программирования с произвольным числом перерывов, а их начало может быть любым в рамках заданных временных окон. Для оптимизации автопарка разработан алгоритм, последовательно сокращающий число привлекаемых ТС. При заданном автопарке минимизация затрат на доставку грузов производится методами локального поиска. На рисунке представлено решение для задачи с 1000 клиентами и 19 транспортными средствами с привязкой к карте г. Новосибирска. |
|
|
Разработка модуля балансировки
нагрузки в рамках проекта «Производство и тестирование платформы Заказчик: Компания Parallels, Новосибирск, 2014. |
|
|
Разработан алгоритм балансировки нагрузки на сервисные узлы хранилища, снижающий число отказов при обработке пользовательских запросов, обусловленных превышением аппаратных возможностей оборудования. Постановка задачи: На загрузку сервисного узла влияют такие параметры, как: - Количество серверов в кластере; - Количество групп информационно-программных ресурсов (ИПР); - Время выполнения задачи; - Аппаратные характеристики серверов (CPU, RAM, объем дискового пространства, скорость сетевого доступа, скорость дискового ввода-вывода, и т. д.); Известны характеристики серверов, начальное распределение групп ИПР между серверами, а также прогнозируемая нагрузка, создаваемая запросами к каждой из групп по каждой из аппаратных характеристик, на протяжении планового периода. Необходимо путем перераспределения групп ИПР между серверами минимизировать суммарное превышение предельно допустимых значений нагрузки. |
 |
Задача выбора оптимального парка сельскохозяйственных машин, выпускаемых крупной машиностроительной компанией Заказчик: компания John Deere (США), 2003 |
|
|
Построена система поддержки принятия решений (СППР), разработанная в ходе выполнения прикладной НИР по заказу одной из крупных компаний, выпускающих машины для сельского хозяйства. В качестве интеллектуального ядра СППР построена математическая модель двухуровневого целочисленного программирования, тесно связанная с задачей о р-медиане с предпочтениями клиентов. Использование разработанной СППР позволило сократить номенклатуру выпускаемых сельскохозяйственных машин и увеличить прибыль компании. Постановка задачи: Крупная машиностроительная компания выпускает сельскохозяйственные машины. Известен список типов машин, выпуском которых занимается или могла бы заниматься данная компания, а также множество групп клиентов, покупающих эти машины. Под группой клиентов понимаем покупателей, объединенных общими производственными целями (например, выращивание зерна в черноземной зоне) и характеризующихся одинаковым поведением на рынке сельхозтехники. В частности, покупатели из одной группы предпочитают один и тот же тип машин, если он есть в продаже, или готовы заменить его на другой согласно предпочтениям, одинаковым для всех покупателей из данной группы, если этот тип отсутствует в продаже. Предполагается, что эти предпочтения распространяются не на все типы из списка, а только на некоторую его часть, т. е. покупатель из группы не покупает ничего у данной компании, если она не выпускает машины из нужного ему списка. Другими словами, все покупатели из группы уйдут к конкурентам компании, если машины из нужного им списка выпускаться не будут. Если же покупатель нашел нужную машину в списке выпускаемой продукции, то он делает заказ и тем самым приносит доход компании. |
 |
| Производство и продажа машин требует от компании определенных затрат, которые состоят из трех частей: затраты на выпуск машин каждого типа, затраты на организацию производства заданного подмножества типов машин и фиксированные затраты на содержание самой компании. Чтобы не потерять клиентов компания должна стремиться выпускать как можно больше типов машин. Однако, в этом случае вторая часть в затратах может оказаться неоправданно большой и прибыль компании упадет. Задача состоит в том, чтобы выбрать такое подмножество типов машин, чтобы, несмотря на потерю части клиентов, добиться максимальной прибыли от продаж. | |