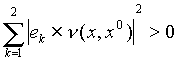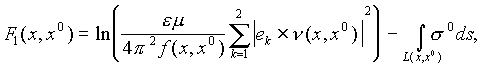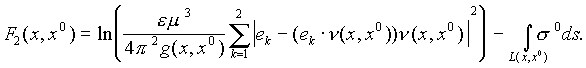As an emergent technology, industrial process tomography is now about 10 years old. At first, X-ray tomography found its application in medicine and then in industry. At present, tomography is intensively employed in non-destructive testing and in flaw detection. The need for a simple, cheap, and environment-friendly technology of monitoring internal structure of objects gave start to development of new methods of tomography. There is now a growing interest to such an area as electromagnetic tomography. The presented paper suggests basic principles of 3-dimensional electromagnetic monitoring by measuring the dynamic of electromagnetic field on a surface enclosing the 3-dimensional object. These principles are based on the following recent research results:
recovering structure of inhomogeneous electromagnetic media by the measurement of the dynamic of electromagnetic fields in domains accessible to observation;
construction of efficient and stable algorithms solving different problems of computerized tomography;
a possibility to measure the dynamic of electromagnetic fields with high accuracy and resolution.
Below we consider one of the problems of electrical conductivity determination of inhomogeneous electromagnetic medium which is inside a 3-dimensional ball, given the dynamic of the electromagnetic field on the surface of this ball. We show that this problem can be reduced to a computerized tomography problem for which we can use well-known, efficient, stable numerical methods [1], [2].
Let us consider the 3-dimensional space of x=(x1, x2, x3)I R3 and assume that it contains inhomogeneous electromagnetic medium. We suppose that dielectric and magnetic permeabilities m and e of this medium are constants, and the conductivity s (x) is a smooth function of a space point x. Moreover, we assume also that this function s (x) equals s 0 (a constant) outside some domain D, and is unknown function of three arguments inside D. The boundary of the domain D is unknown also, but it is known, that D is enclosed a ball of some fixed radius l, i.e. D I D(l)={x I R3 | | x| < l}.
The current density has the form
J = s (x)E + J0,
here J0 is the external current density having the form
J0 = ed (x- x0) * d (t),
where e is a fixed vector of the 3-dimensional space; x0 is a point of the sphere S(l) = {xI R3 | | x| = l}.
It can be noticed that this point x0 can run the surface S(l), being the parameter of the experiment:
d (x- x0) = d (x1- x10) * d (x2- x20) * d (x3- x30)
where d (? ) is the Dirac–delta function.
Remark 1. The internal current of the form J0=ed (x- x0) * d (t) is a pulse directional source which is concentrated in the point x = x0 at the moment t = 0 in the direction of the vector e.
We will denote through Ek(x, t, x0), Hk(x, t, x0) the electric and magnetic intensity vectors corresponding to the external current J0 with the directional vector e = ek, where ek is k-th basis vector of R3, i.e. e1=(1, 0, 0), e2=(0, 1, 0), e3=(0, 0, 1).
We define the functions F(x, x0, t), G(x, x0, t) by equalities
,
,
where
.
The main objective of the study is to determine the domain D and, for x I D, the function s (x), if one of the functions F(x, x0, t) or G(x, x0, t) is known for all x I S(l), x0 I S(l), t I [t (x, x0) - w , t (x, x0) + w ] where w is a fixed positive number.
Let g(x, x0), f(x, x0), n (x, x0) be the functions defined by the equalities
,
,

It was shown in [3] that in the first case, the following inequalities take place g(x, x0) > 0, f(x, x0) > 0, and
,
in the second case, the stated problem can be reduced to one of the following tomography problems:
(1)
(2)
where
and
L(x, x0) is the segment of the straight line which connects x and x0.
To solve the obtained tomography problems (1) and (2), recent numerical techniques can be used such as [1], [2].
We conclude by remarking that, for different applications, the original statement of the problem may be quite different. It is possible to reduce a lot of problems of that kind to the standard computerized tomography problem.
The presented technology of electromagnetic monitoring can be applied in medicine, non-destructive testing, flaw detection.
References
1. Natterer F. The Mathematics of Computerized Tomography -Stuttgart, John Wiley & Sons Ltd and B.G. Teubner, 1986.-222,p.
2. Trofimov O. Numerical Algorithms of Tomography on Base Distributions // Proceedings of 15-th World Congress on Scientific Computation, Modelling and Applied Mathematics-Berlin, August 1997, Wissenschaft & Technik Verlag-v.3,-p.707-711.
3. Yakhno V.G. Multidimensional Inverse Problems in Ray Formulation for Hyperbolic Equtions // Inverse and Ill-posed Problems, VSP, Utrecht, The Netherlands,1998-v.6,3-p.71-85.