Метод наименьших квадратов

Предположим, что вектор ошибок $\text{\boldmath\ensuremath \varepsilon}$ состоит из независимых случайных величин с нормальным распределением ${\mathsf N}_{0,\sigma^2}$ . Функция правдоподобия (30) имеет вид

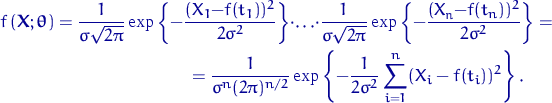
$\begin{multline*} f\left({\mathbf X};\text{\boldmath\ensuremath \theta}\right)=\... ...xp\left\{-\dfrac{1}{2\sigma^2}\sum_{i=1}^n(X_i-f(t_i))^2\right\}.\end{multline*}$

Очевидно, что при любом фиксированном $\sigma^2$ максимум функции правдоподобия достигается при наименьшем значении суммы квадратов ошибок $\sum(X_i-f(t_i))^2=\sum\varepsilon_i^2$ .

Определение 31.

Оценкой метода наименьших квадратов (ОМНК) для неизвестных параметров $\theta_1,\ldots,\theta_k$ уравнения регрессии называется набор значений параметров, доставляющий минимум сумме квадратов отклонений

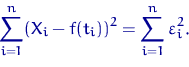
$\begin{displaymath} \sum_{i=1}^n(X_i-f(t_i))^2=\sum_{i=1}^n\varepsilon_i^2.\end{displaymath}$

Найдя оценки для $\theta_i$ , найдем тем самым оценку $\hat f(t)$ для

. Обозначим через $\hat{f}(t_i)$ значения этой функции, и через $\hat\varepsilon_i=X_i-\hat{f}(t_i)$ соответствующие оценки ошибок. Оценка максимального правдоподобия для $\sigma^2$ , она же точка максимума по $\sigma^2$ функции правдоподобия, равна вычислить!

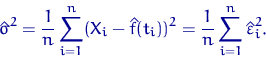$\begin{equation} \hat\sigma^2=\dfrac{1}{n}\sum_{i=1}^n(X_i-\hat{f}(t_i))^2= \dfrac{1}{n}\sum_{i=1}^n \hat\varepsilon_i^2.\end{equation}$

(31)

Мудрый читатель понял, что основная цель рассмотренного выше примера — показать, что метод наименьших квадратов не падает с неба, а есть в точности метод максимального правдоподобия в случае, когда вектор ошибок, а вместе с ним и вектор наблюдаемых откликов регрессии, состоит из независимых и одинаково распределенных случайных величин с нормальным распределением.

Пример 34.

Пусть плотность независимых случайных величин $\varepsilon_i$ имеет вид

$\begin{displaymath} h(x)=\dfrac{1}{2\sigma}~\exp\left\{-\lvert x \rvert/\sigma\r... ...}\end{displaymath}$

т.е. $\varepsilon_i$ имеют распределение Лапласа. Тогда при любом фиксированном $\sigma^2$ максимум функции правдоподобия достигается при наименьшем значении суммы

$\sum \lvert X_i-f(t_i) \rvert$

абсолютных отклонений. Оценка максимального правдоподобия (ОМП) для набора $\theta_1,\ldots,\theta_k$ уже не есть ОМНК.

9.3. Метод наименьших квадратов