 |
|
Sobolev Institute of Mathematics, Novosibirsk, Russia
Let ![]() be i.i.d. random variables satisfying
the conditions
be i.i.d. random variables satisfying
the conditions ![]() and
and ![]() . Let
. Let
![]() be a sequence of real numbers. Define the
stationary sequence of random variables
be a sequence of real numbers. Define the
stationary sequence of random variables ![]()
![]() and the corresponding partial sum process:
and the corresponding partial sum process:

![]()
![]()

![]()
Theorem. Let the sequence ![]() be summable and
be summable and

Moreover, let one of the following two conditions be valid:
Then the sequence ![]()
![]() -converges in
-converges in ![]() to a standard Wiener process.
to a standard Wiener process.
Note that this Theorem improves the corresponding results in [1-3].
Namangan Engineering-Pedagogical Institute, Namangan, Uzbekistan
Let ![]() be a stochastic process with independent stationary
increments,
be a stochastic process with independent stationary
increments, ![]() ,
, ![]() . Given arbitrary
. Given arbitrary ![]() and
and ![]() , we define the random variables and respectively equal to the number of crossings of a strip
, we define the random variables and respectively equal to the number of crossings of a strip ![]() on the coordinate plane of points
on the coordinate plane of points ![]() from below to
above and from above to below by the sample paths of the random walk
with continuous time
from below to
above and from above to below by the sample paths of the random walk
with continuous time ![]() over the time interval from 0 to
over the time interval from 0 to ![]() .
.
We study asymptotic behavior of the distribution of random variables
and as ![]() ,
,![]() , and
, and ![]() . The final result consists in
complete asymptotic expansions of the probabilities
. The final result consists in
complete asymptotic expansions of the probabilities
![]() ,
, ![]() , under various restrictions on
, under various restrictions on ![]() ,
, ![]() ,and
,and ![]() compatible with the condition
compatible with the condition ![]() . This problem
was solved in [1] for the discrete time case. Here we use the methods
and technique of [1]. The asymptotics of the distribution of the
random variables
. This problem
was solved in [1] for the discrete time case. Here we use the methods
and technique of [1]. The asymptotics of the distribution of the
random variables ![]() in the cases when they are finite
was studied in [2].
in the cases when they are finite
was studied in [2].
We suppose here that ![]() and the Cramer condition holds
on the analyticity of the function
and the Cramer condition holds
on the analyticity of the function ![]() in a
strip containing the imaginary axis. Moreover, we impose some
conditions of [3] which provide some necessary properties of components of
infinitely divisible factorization of the function
in a
strip containing the imaginary axis. Moreover, we impose some
conditions of [3] which provide some necessary properties of components of
infinitely divisible factorization of the function ![]() .
.
Novosibirsk State University, Novosibirsk, Russia
The asymptotic behavior of wide class of additive functionals of order statistics is investigated.
In particular,
strong law of large numbers for linear combinations of functions of order statistics (![]() -statistics)
based on weakly dependent random variables is proven.
As an auxiliary result we
establish the Glivenko-Cantelli theorem for
-statistics)
based on weakly dependent random variables is proven.
As an auxiliary result we
establish the Glivenko-Cantelli theorem for ![]() -mixing sequences of identically distributed
random variables.
Also, asymptotic normality of a class of spacings statistics based on independent and
identically distributed random variables is obtained.
-mixing sequences of identically distributed
random variables.
Also, asymptotic normality of a class of spacings statistics based on independent and
identically distributed random variables is obtained.
DI - Ecole Normale Supérieure, Paris, France
On a locally finite point set, a navigation defines a path through
the point set from a point to an other. The set of paths leading to
a given point defines a tree, the navigation tree. In this talk,
we will analyze the properties of the navigation tree when the point set
is a Poisson point process on ![]() . We examine the distribution of
stable functionals, the local weak convergence of the navigation
tree, the asymptotic average of a functional along a path, the shape
of the navigation tree and its topological ends. We illustrate our
work in the small world graphs, and new results are established.
. We examine the distribution of
stable functionals, the local weak convergence of the navigation
tree, the asymptotic average of a functional along a path, the shape
of the navigation tree and its topological ends. We illustrate our
work in the small world graphs, and new results are established.
Sobolev Institute of Mathematics, Novosibirsk, Russia
Let ![]() be a stationary sequence of
be a stationary sequence of
![]() -uniformly distributed r.v.'s,
-uniformly distributed r.v.'s, ![]() .Introduce the class of normalized
.Introduce the class of normalized ![]() -variate von Mises
statistics:
-variate von Mises
statistics:
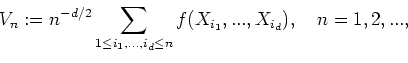
Theorem. Let ![]() and, moreover, let
and, moreover, let
![]() be
square-integrable on all diagonal subspaces of the unit cube
be
square-integrable on all diagonal subspaces of the unit cube ![]() w.r.t. the corresponding induced Lebesgue measures.
If the sequence
w.r.t. the corresponding induced Lebesgue measures.
If the sequence ![]() satisfies
satisfies ![]() -mixing condition
with following restrictions on the corresponding coefficient:
-mixing condition
with following restrictions on the corresponding coefficient:
![]() then
then
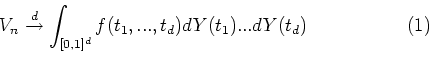
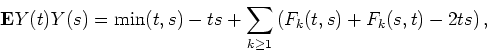
In the talk, under less restrictive mixing conditions of the observations (but for more narrow subclass of the kernels), we study another representation of the limit distribution for these statistics as infinite polynomials of dependent Gaussian random variables. In the i.i.d. case this duality representation of the limit distribution is well known.
Sobolev Institute of Mathematics, Novosibirsk, Russia
Let
![]() be a nonempty set and
be a nonempty set and ![]() be a semiring of its subsets with
identity. Let
be a semiring of its subsets with
identity. Let ![]() be a random process
defined on a probability space
be a random process
defined on a probability space ![]() and
satisfying the condition
and
satisfying the condition ![]() for all
for all ![]() The process
The process ![]() is called an elementary stochastic
measure or a noise if
is called an elementary stochastic
measure or a noise if
![]()

As an application of the above-mentioned general scheme, we also study multiple stochastic integrals of the form

In the second part of the talk we discuss some applications
of this construction to asymptotic
analysis of normalized canonical von Mises statistics
and U-statistics based
on samples from a stationary sequence of observations
under some dependency conditions.
Sobolev Institute of Mathematics, Novosibirsk, Russia
A huge number of papers are devoted to the study of large deviation (l.d.) problems for sums of i.i.d. random variables. In spite of this until very recent times the systematical unified approach to the solution of these problems was absent and some problems remained to be open.
Let ![]() be i.i.d. random variables,
be i.i.d. random variables,
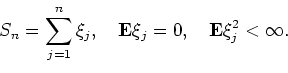
If the right hand side Cramer condition is met:
![]()

The talk exposes the systematical unified approach to the solution of all principal l.d. problems in all areas of l.d. The approach is based on the following elements:
Sobolev Institute of Mathematics, Novosibirsk, Russia
Suppose we are given a sample
![]() consisting of
consisting of ![]() independent observations
in an arbitrary measurable space
independent observations
in an arbitrary measurable space ![]() such that
the first
such that
the first ![]() observations have a common distribution
observations have a common distribution
![]() , and the remaining
, and the remaining ![]() a distribution
a distribution
![]() . The distributions
. The distributions ![]() and
and ![]() are unknown, and both
are unknown, and both ![]() and
and ![]() are assumed large.
Under certain assumptions on
are assumed large.
Under certain assumptions on ![]() and
and ![]() concerning
either their moments or the behavior of their tails
we construct estimates
concerning
either their moments or the behavior of their tails
we construct estimates ![]() for the change point
for the change point
![]() with a ``proper'' error, i.e., such that
with a ``proper'' error, i.e., such that
![]() converges to zero
with growing
converges to zero
with growing ![]() (at an exponential or polynomial rate).
In the problem of sequential estimation of
(at an exponential or polynomial rate).
In the problem of sequential estimation of ![]() we construct a stopping time
we construct a stopping time ![]() with explicit bounds for
with explicit bounds for ![]() , for which asymptotics of
, for which asymptotics of ![]() as
as ![]() is found
within
is found
within ![]() (or within a constant if the distributions
(or within a constant if the distributions
![]() and
and ![]() are unknown).
are unknown).
Sobolev Institute of Mathematics, Novosibirsk, Russia
Let ![]() be i.i.d. random variables,
be i.i.d. random variables,
![]()
![]()
Integro-local and integral limit theorems for ![]() are
obtained. They describe for any fixed
are
obtained. They describe for any fixed ![]() the exact asymptotics of
the exact asymptotics of
![]()
Sobolev Institute of Mathematics, Novosibirsk, Russia
Let ![]() be positive i.i.d. random variables,
be positive i.i.d. random variables,
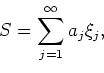
(i) sequence ![]() is regularly varying with exponent
is regularly varying with exponent
![]() , and
, and ![]() as
as ![]() for some
for some ![]() ,
,
(ii) ![]() is regularly varying with exponent
is regularly varying with exponent
![]() as
as ![]() , and
, and ![]() as
as ![]() for
some
for
some ![]() ,
,
(iii) ![]() and
and ![]() are regularly varying
with positive exponents (as
are regularly varying
with positive exponents (as ![]() and
and ![]() , respectively).
, respectively).
We show, in particular, that the asymptotics of ![]() as
as ![]() can be expressed as the product of known constant
can be expressed as the product of known constant ![]() and
function
and
function ![]() , where
, where ![]() depends on
depends on ![]() ,
, ![]() , and coefficients
, and coefficients ![]() , whereas
, whereas ![]() is determined only by the asymptotics of:
is determined only by the asymptotics of:
The asymptotics of ![]() ,
, ![]() , is
refined provided that
, is
refined provided that ![]() is the geometric progression and
is the geometric progression and
![]() as
as
![]() ,
, ![]() ,
, ![]() .
.
EURANDOM, Eindhoven, The Netherlands
Joint work with Vsevolod Shneer (Novosibirsk, Russia & Edinburgh, UK)
We present exact asymptotics for the distribution of the first time a Levy process becomes negative, starting from positive level. We apply these results to find asymptotics for the distribution of the busy period in an M/GI/1 queue.
Weierstrass Institute for Applied Analysis and Stochastics, Berlin, Germany
Let ![]() denote a Galton-Watson process with
denote a Galton-Watson process with ![]() .We restrict attention to the supercritical case with
.We restrict attention to the supercritical case with
![]() . It is well-known that there exist
constants
. It is well-known that there exist
constants ![]() such that
such that
![]()
Romanovskii Institute of Mathematics, Tashkent, Uzbekistan
It is well known that the classical theory of summation of independent random variables is based on the condition of uniform infinite smallness (UN-condition). Under this condition the class of limiting distributions for sums of independent random variables coincides with the class of infinitely divisible distributions. Nevertheless, P. Levy noticed long ago that UN-condition is inessential if we consider the convergence to a fixed limiting distribution.
Limit theorems for distributions of sums of independent random variables proved without UN-condition are called non-classical. This terminology was introduced by V. M. Zolotarev who proved a non-classical version of central limit theorem that generalized the classical Lindeberg-Feller theorem.
Our talk contains non-classical versions of the central limit theorem and the theorem on the convergence to the Poisson distribution in terms of characteristic functions of summands. The proofs of our theorems use modified versions of the well-known Stein-Tikhomirov and Stein-Chen methods. Moreover, the modifications of the above-indicated methods are connected with solutions of characterization problems for the Gaussian and Poisson distributions in terms of characteristic functions.
The theorems presented in the talk can be generalized for sequences of independent random variables taking values in separable Hilbert spaces. In addition, we prove some non-classical theorems on the convergence of the distributions of sums of independent random variables that provide the convergence of the moments of an arbitrary order.
Sobolev Institute of Mathematics, Novosibirsk, Russia & Heriot-Watt University, Edinburgh, UK
We present a short new proof of the following result.
Let ![]() be a distribution on the positive half-line and
be a distribution on the positive half-line and
![]() . Assume that, for
any
. Assume that, for
any ![]() ,
,
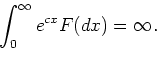
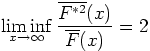
We also provide various comments or relative problems.
Based on joint work with D. Denisov and D. Korshunov.
Omsk State University, Omsk, Russia
Let ![]() be a strictly stationary
sequence,
be a strictly stationary
sequence, ![]() and
and
![]() . Denote
. Denote
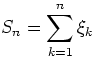 ,
, ![]() .
If random
variables
.
If random
variables ![]() ,
, ![]() ,
, ![]() and
and ![]() have
density functions
have
density functions ![]() ,
, ![]() and
and ![]() , then
the symbol
, then
the symbol ![]() denotes that
denotes that
![]() ,
,
![]() as
as
![]() .
.
Let ![]() stand for the standard normal random
variable. We say that the local limit theorem is applicable to the
sequence
stand for the standard normal random
variable. We say that the local limit theorem is applicable to the
sequence ![]() , if for each
, if for each ![]() random variables
random variables ![]() have
densities and
have
densities and ![]() .
.
The sequence ![]() is called regularly varying with
exponent
is called regularly varying with
exponent ![]() , if is a regularly varying function
with exponent
, if is a regularly varying function
with exponent ![]() (here
(here ![]() is the greatest integer not greater
is the greatest integer not greater ![]() ).
We denote by
).
We denote by ![]() independent
random variables with the same distributions as
independent
random variables with the same distributions as
![]() . The symbol
. The symbol ![]() means that
means that
![]() and
and ![]() is an arbitrary sequence of positive
integers.
is an arbitrary sequence of positive
integers.
Theorem 1.
The local limit theorem is applicable to ![]() and
and ![]() is regularly varying with exponent
is regularly varying with exponent ![]() if and only if
if and only if
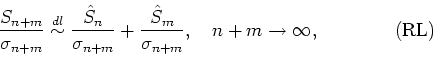
![]() is uniformly
integrable,
is uniformly
integrable,
![]() ,
,
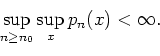
Theorem 1 can be interpreted as follows. (RL) is the minimal
condition of weak dependence for the sequence ![]() providing
applicability the local limit theorem with regularly varying
providing
applicability the local limit theorem with regularly varying
![]() with
the exponent
with
the exponent ![]() .
.
Replacing ![]() by stochastic equivalence in (RL), we get the
minimal condition for central limit theorem (see [1]).
by stochastic equivalence in (RL), we get the
minimal condition for central limit theorem (see [1]).
St. Petersburg Department of Steklov Mathematical Institute,
Saint-Petersburg, Russia
In this talk we consider a few problems of statistical estimation of analytic functions (analytic function observed in an additive noise, estimation of analytic distribution density function, estimation of analytic spectral density function). The problems concerne the unicity theorem for analytic functions. An analytic function is fully determined by its values on an interval. We study how stable is the theorem with respect to the abovementioned random perturbations.
Al-Farabi Kazakh National University, Almaty, Kazakhstan
Let ![]() ,
, ![]() , be two
independent sequences of independent random variables
identically distributed within each sequence.
Introduce a random walk with one level of switching
, be two
independent sequences of independent random variables
identically distributed within each sequence.
Introduce a random walk with one level of switching ![]() as
follows:
as
follows: ![]() and given
and given ![]() , put
, put

It is assumed that jumps from positions that are below point ![]() have a
negative mean
have a
negative mean ![]() (then the random walk may drift
to minus infinity with a positive probability) and that there are
exponential moments for the distributions of jumps
(then the random walk may drift
to minus infinity with a positive probability) and that there are
exponential moments for the distributions of jumps ![]() ,
, ![]() (the so-called light-tailed case).
(the so-called light-tailed case).
Let ![]() ,
, ![]() be arbitrary numbers and
be arbitrary numbers and ![]() . I study tail asymptotics for the distribution of the supremum
. I study tail asymptotics for the distribution of the supremum
![]() , as
, as ![]() and
and ![]() .
.
The stable case where jumps from positions that are below point
![]() have a positive mean and jumps from positions that are above
point
have a positive mean and jumps from positions that are above
point ![]() have a negative mean has been studied by A.A.Borovkov
and D.A.Korshunov. In this situation a stationary distribution
always exists. A.A.Borovkov (1980) has found the
Laplace-Stieltjes transform for this stationary distribution.
A.A.Borovkov and D.A.Korshunov (1996, 2001, 2002) considered a
more general class of "asymptotically homogenous" Markov chains
and derived a number of large deviations results for their
stationary distributions. D.V.Gusak, O.I.Eleiko (1981) and
N.S.Bratiychuk, D.V.Gusak, O.I.Eleiko (1984) have found the
Laplace-Stieltjes transforms for the supremum of a random walk
with one level of switching model for some special types of walks.
I am unaware of any other results on (asymptotic) behavior of the
supremum.
have a negative mean has been studied by A.A.Borovkov
and D.A.Korshunov. In this situation a stationary distribution
always exists. A.A.Borovkov (1980) has found the
Laplace-Stieltjes transform for this stationary distribution.
A.A.Borovkov and D.A.Korshunov (1996, 2001, 2002) considered a
more general class of "asymptotically homogenous" Markov chains
and derived a number of large deviations results for their
stationary distributions. D.V.Gusak, O.I.Eleiko (1981) and
N.S.Bratiychuk, D.V.Gusak, O.I.Eleiko (1984) have found the
Laplace-Stieltjes transforms for the supremum of a random walk
with one level of switching model for some special types of walks.
I am unaware of any other results on (asymptotic) behavior of the
supremum.
Omsk Branch of Sobolev's Institute of Mathematics SB RAS, Omsk, Russia
We consider a population of a fixed size ![]() where each particle
has a type ascribed to it. In integer time moments each particle
generates a random number of offspring of the same type in such a
way that the population keeps its size constant and joint
distributions of offspring numbers are exchangeable.
where each particle
has a type ascribed to it. In integer time moments each particle
generates a random number of offspring of the same type in such a
way that the population keeps its size constant and joint
distributions of offspring numbers are exchangeable.
Let ![]() be the number of offspring produced by one
particle,
be the number of offspring produced by one
particle, ![]() ,
and
,
and ![]() .
.
Several upper estimates for expected fixation time ![]() , i.e.
the random time when all the particles have one type, are obtained
for an arbitrary initial configuration of particles.
, i.e.
the random time when all the particles have one type, are obtained
for an arbitrary initial configuration of particles.
Theorem. Let an initial population have ![]() particles of j-th type,
particles of j-th type, ![]() ,
, ![]() , and
, and ![]() . There exists a sequence
. There exists a sequence
![]() ,
, ![]() , such that
, such that
![]() and
and
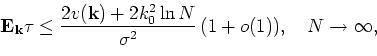
![]() . Particularly, if
. Particularly, if ![]() ,
, ![]() , then
, then ![]() ,
, ![]() .
.
![]() Supported by grants: RFBR-NWO 047.016.013, RFBR 06-01-00127, Russian Scientific School 4129.2006.1
Supported by grants: RFBR-NWO 047.016.013, RFBR 06-01-00127, Russian Scientific School 4129.2006.1
Novosibirsk State Technical University, Novosibirsk, Russia
A Sign Method of correlation function estimation of a zero-mean Gaussian stationary series is based on calculation of a frequence of a sign change of series' elements.
If the stationary series is a Fractional Gaussian Noise (FGN),
that is, a variance of its particular sums grows as ![]() ,
then a probability of a sign change does not depend on an analysing
object to be an initial series or series of sums of a fixed number of elements:
if
,
then a probability of a sign change does not depend on an analysing
object to be an initial series or series of sums of a fixed number of elements:
if ![]() is a FGN then for any fixed
is a FGN then for any fixed ![]()
![]()
Thus one can made an estimator of ![]() better by an aggregation
of the random series, that is, by fixing a set of divisions
of the series on blocks of an equal size.
better by an aggregation
of the random series, that is, by fixing a set of divisions
of the series on blocks of an equal size.
We propose an algorithm of search of an aggregation giving an
asymptotically minimal variance in the case ![]() . In this case
the random sequence is a sample from a normal distribution with a zero mean.
. In this case
the random sequence is a sample from a normal distribution with a zero mean.
This algorithm is a solution of a problem of quadratic programming with Boolean variables. We give examples of the algorithm's realizations under different restrictions on a maximal block size.
University of Illinois, Urbana, USA
What guidance can information theory provide to the emerging technologies of wireless and sensor networks that may be at the cusp of a possible takeoff? This talk explores the themes of how much information wireless networks can transport, what should be their architecture, what protocols are appropriate for their operation, and a possible Maxwellian model of computation for sensor networks.
St.Petersburg State University, Russia & Université Paris VI, France
Consider a planar Brownian
motion starting from an interior point of the parabolic domain
![]() , and let
, and let ![]() denote the first time
the Brownian motion exits from
denote the first time
the Brownian motion exits from ![]() . The tail behaviour [or
equivalently, the integrability property] of
. The tail behaviour [or
equivalently, the integrability property] of ![]() is
somewhat unusual since it arises from an interference of large
deviation and small deviation events. Our main result implies
that the limit of
is
somewhat unusual since it arises from an interference of large
deviation and small deviation events. Our main result implies
that the limit of ![]() [as
[as ![]() ] exists and equals
] exists and equals ![]() , thus improving
previous estimates by Bañuelos et al. (2001) and W. Li (2003).
The existence of the limit is proved by applying the classical
Schilder large deviation theorem. The identification of the limit
leads to a variational problem, which is solved by exploiting a
theorem of Biane and Yor (1987) relating different additive
functionals of Bessel processes. Our result actually applies to
more general parabolic domains in any finite dimension
, thus improving
previous estimates by Bañuelos et al. (2001) and W. Li (2003).
The existence of the limit is proved by applying the classical
Schilder large deviation theorem. The identification of the limit
leads to a variational problem, which is solved by exploiting a
theorem of Biane and Yor (1987) relating different additive
functionals of Bessel processes. Our result actually applies to
more general parabolic domains in any finite dimension ![]() , namely
, namely
![]()
Sobolev Institute of Mathematics, Novosibirsk, Russia
Let ![]() be a sequence of i.i.d. random variables,
be a sequence of i.i.d. random variables,
![]() ,
, ![]() . For
. For ![]() and
and ![]() we consider the
sojourn time
we consider the
sojourn time

The problem consists of studying the joint distribution ![]() .
.
Denote ![]() and
and

We prove that, for ![]() and
and ![]() ,
,
![]()
This equation contains two unknown functions. Using a Wiener-Hopf
type method we solve it and find ![]() in terms of certain operators
containing double transforms of joint distributions of ladder
heights and ladder epochs. The representations for
in terms of certain operators
containing double transforms of joint distributions of ladder
heights and ladder epochs. The representations for ![]() obtained in
this way look rather complicated so we give asymptotic formulas for
them under Cramer condition, as
obtained in
this way look rather complicated so we give asymptotic formulas for
them under Cramer condition, as ![]() and
and ![]() . The
main parts of these asymptotic formulas can be used for direct
inversion or for asymptotic analysis of probabilities.
. The
main parts of these asymptotic formulas can be used for direct
inversion or for asymptotic analysis of probabilities.
Kurgan University, Kurgan, Russia
Let ![]() be a homogeneous Markov chain
with state space
be a homogeneous Markov chain
with state space
![]() and transition matrix
and transition matrix
![]() .For any subset
.For any subset
![]() consider the random set
consider the random set
![]()
![]()
![]()
With help
of these functionals, by varying set ![]() we get a wide class of functionals
for chain
we get a wide class of functionals
for chain ![]() . Some of these functionals, especially in the case
. Some of these functionals, especially in the case
![]() , are researched in much detail
(see [1]-[3] and references there).
, are researched in much detail
(see [1]-[3] and references there).
For the matrix
![]() and the set
and the set ![]() put
put
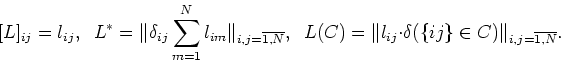
In the sequel we shall assume that all essential states
of ![]() are aperiodic states. Under this assumption we denote
are aperiodic states. Under this assumption we denote
![]() . The following statement holds:
. The following statement holds:
Theorem 1.
For ![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
Expressions for factorial moments of the functional ![]() are given in
report. The next assertions are proved too.
are given in
report. The next assertions are proved too.
Theorem 2.
For ![]()
![]()
Theorem 3.
Let
![]() be an arbitrary essential state of
be an arbitrary essential state of ![]() or
or
![]() be the nonessential state of
be the nonessential state of ![]() such that
such that
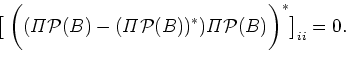
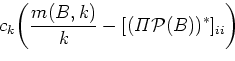
Ufa State Aviation Technical University, Ufa, Russia
Consider a Wiener process ![]() with the jointly continuous local time
with the jointly continuous local time
![]() ,
, ![]() ,
, ![]() ,put
,put ![]() ,
, ![]() ,
, ![]() . Let
. Let ![]() be an arbitrary function, denote
be an arbitrary function, denote
![]()
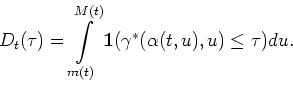
Generalized Ito formula is proved for left-continuous
predictable functions ![]() and for a Wiener process
and for a Wiener process ![]() .
.
Theorem 1. Let ![]() ,
, ![]() , be a
standard Wiener process. Then
, be a
standard Wiener process. Then
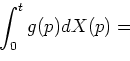
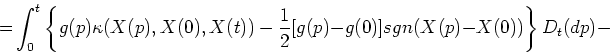

![]() be arbitrary left continuous predictable functions,
such that Ito and Lebesgue-Stieltjes integrals in (1) are finite. It is
proved that the limits (in probability) in right-side part of
formula (1) always exist.
be arbitrary left continuous predictable functions,
such that Ito and Lebesgue-Stieltjes integrals in (1) are finite. It is
proved that the limits (in probability) in right-side part of
formula (1) always exist.
We have to notice that right-side part of the formula (1) is valid
for unpredictable left-continuous functions ![]() and arbitrary
continuous functions
and arbitrary
continuous functions ![]() , which admit the jointly continuous local
time
, which admit the jointly continuous local
time ![]() ,
, ![]() ,
, ![]() . Hence the
formula (1) allows to define Ito type integrals for unpredictable
integrands and continuous functions
. Hence the
formula (1) allows to define Ito type integrals for unpredictable
integrands and continuous functions ![]() .
.
![]() Supported by RFFI grants 04-01-00286-a, 05-01-97909.
Supported by RFFI grants 04-01-00286-a, 05-01-97909.
VTT Technical Research Centre of Finland
Joint work with Petteri Mannersalo and Michel Mandjes
Consider a fluid queue with two priority classes. We show that the event that the low priority queue exceeds a level and the event that the delay of a fluid molecule exceeds a level can both be written in the form of a union of intersections of elementary univariate events related to the cumulative input processes. In "many sources" -type large deviation limits of these events, the respective dominating points (most probable paths) minimizing the rate function are characterized as those of infinite intersections of simple events. More exactly, the basic problem turns out to be the identification of the most probable path that lies above a straight line on a certain interval. In the case that the input processes are Gaussian, the dominating points can be computed more explicitly, since the problem is then a minimum norm problem in the reproducing kernel Hilbert space. A general technique to solve this problem is presented.
Wroclaw University, Wroclaw, Poland
In this talk we consider the optimal dividend problem for an insurance company whose risk process evolves as a spectrally negative Lévy process in the absence of dividend payments. The classical dividend problem for an insurance company consists in finding a dividend payment policy that maximizes the total expected discounted dividends. Related is the problem where we impose the restriction that ruin be prevented: the beneficiaries of the dividends must then keep the insurance company solvent by bail-out loans. Drawing on the fluctuation theory of spectrally negative Lévy processes we give an explicit analytical description of the optimal strategy in the set of barrier strategies and the corresponding value function, for either of the problems. Subsequently we investigate when the dividend policy that is optimal amongst all admissible ones takes the form of a barrier strategy.
Central Economics & Mathematics Institute of RAS, Moscow, Russia
Let a sequence of the random variables ![]() forms
a supermartingale defined on a filtered probability space
with
forms
a supermartingale defined on a filtered probability space
with ![]() , , i.e.
, , i.e.
![]() .
.
Let 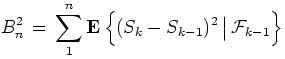 ,
, ![]() ,
, ![]() .
.
Theorem. The following inequality holds:
![]() ,
,
where ![]() ,
,
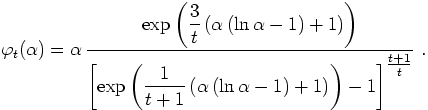
Corollary. Let ![]() be a
martingale,
be a
martingale, ![]()
![]() .
Then
.
Then

The last inequality was obtained by Burkholder in [1] without
explicit expression for ![]() .
.
Let ![]() . For
. For ![]() the
function
the
function ![]() decreases slowly (as
decreases slowly (as ![]() ) from
) from ![]() to
to ![]() , so that
, so that ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
The proofs are based on the modification of the proofs and
results from [2] (see also [3]).
University of Colorado, Denver, USA and IITP, Moscow, Russia
We concern ourselves with studying the large deviation principle (LDP) for queueing networks with homogeneous customer populations. The processes of the exogenous arrivals, service and routing are assumed to be general and are only required to obey LDPs in the associated function spaces with action functionals of integral form. We show that under additional conditions this implies an LDP for the queue length processes and find the action functional explicitly. In particular, an LDP for a broad class of generalised open Jackson networks is obtained. Our approach is based on the large deviation relative compactness property of exponentially tight sequences of probability measures. The action functional is identified in terms of a weak solution to a system of idempotent equations obtained as large deviation limits of the stochastic equations governing the network.
St.Petersburg Chemical-Pharmaceutical Academy, St.Petersburg, Russia
Consider a sequence of independent identically distributed random
variables ![]() , ,
, , ![]() , and denote
, and denote ![]() ,
, ![]() ,
, ![]() .
.
Theorem. For ![]()
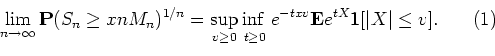
This result is one of the Chernoff type theorems for self-normalized sums of i.i.d. random variables (see also Qi-Man Shao "Self-normalized large deviations", The Annals of Probability 1997, Vol.25, No.1, 285-328).
Note that if ![]() then (1) is identical to the classical Chernoff
theorem as in Bahadur R.R. "Some limits theorems in statistics",
Regional Conference Series in Applied Mathematics 4. SIAM,
Philadelphia.
then (1) is identical to the classical Chernoff
theorem as in Bahadur R.R. "Some limits theorems in statistics",
Regional Conference Series in Applied Mathematics 4. SIAM,
Philadelphia.
![]() The investigations were supported by Grant of Scientific School
No. 4222.2006.1 and RFFI Grant No. 06-01-00179-a.
The investigations were supported by Grant of Scientific School
No. 4222.2006.1 and RFFI Grant No. 06-01-00179-a.
Institute for Information Transmission Problems, Moscow, Russia
We study the Poisson Hypothesis, which is device to analize approximately the behavior of large queuing networks. We prove it in some simple limiting cases. We show in particular that the corresponding dynamical system, defined by the non-linear Markov process, has a lane of fixed points which are global attractors. To do this we derive the corresponding non-linear equation and we explore its self-averaging properties. We also argue that in cases of heavy-tail service times the PH can be violated.
Ugra State University, Khanty-Mansiysk, Russia
Let
![]() be an infinite sequence of independent
random variables with
be an infinite sequence of independent
random variables with ![]() and
and ![]() .Consider a random function
.Consider a random function
![]() such that
such that

Introduce now the main notations
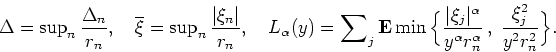
![]()
In the partial case when ![]() and
and ![]() a weaker estimate with
instead of truncated moments
a weaker estimate with
instead of truncated moments ![]() was obtained earlier in [1].
was obtained earlier in [1].
Theorem sharpens also several known results from [2].
Note, that a simple case when
![]() for
for ![]() is also possible in Theorem.
is also possible in Theorem.
Novosibirsk State University of Economics and Management, Novosibirsk, Russia
The model of the financial market consisting of a riskless asset
(bond) ![]() and risk asset (stock)
and risk asset (stock) ![]() is considered.
Their respective prices follow the equations:
is considered.
Their respective prices follow the equations:
![]()
It is well known (see for example [1], [2]) that under standard assumptions (no arbitrage, completeness of financial market etc.) the pricing of financial assets (securities) can be reduced to calculating expectations. The main problem is that if we are not the Black-Scholes setting this calculation becomes a serious technical hurdle.
We consider the use of Fourier-analytic methods for pricing a wide class of securities and give explicit formulae for security prices by means of the Fourier transform. Implications for option pricing are discussed.
Sobolev Institute of Mathematics, Novosibirsk, Russia
Let ![]() be i.i.d. random variables and
be i.i.d. random variables and
![]() be real numbers such that
be real numbers such that ![]() and
and
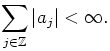 Consider a stationary sequence of random variables
Consider a stationary sequence of random variables ![]() having
a structure of the so-called moving averages:
having
a structure of the so-called moving averages:
 . We study
possible types of mixing for the sequence
. We study
possible types of mixing for the sequence ![]() .
We say that
the sequence
.
We say that
the sequence ![]() satisfies
satisfies ![]() -mixing if
-mixing if

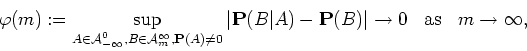
In the talk, we formulate conditions on ![]() and the
distribution of
and the
distribution of ![]() providing (or not!)
providing (or not!) ![]() - or
- or
![]() -mixing of the sequence
-mixing of the sequence ![]() It is clear that if the
set of integers
It is clear that if the
set of integers ![]() is finite then, for some
natural
is finite then, for some
natural ![]() , the sequence
, the sequence ![]() consists of
consists of ![]() -dependent random
variables (i.e., satisfies the mixing conditions above). In the
opposite case we obtained the following results.
-dependent random
variables (i.e., satisfies the mixing conditions above). In the
opposite case we obtained the following results.
Proposition 1. Let ![]() be a bounded random
variable having a continuous density, and
be a bounded random
variable having a continuous density, and ![]()
![]() . Then the
sequence
. Then the
sequence ![]() satisfies
satisfies ![]() -mixing.
-mixing.
Proposition 2. Let ![]() be a discrete random
variable with a finite number of atoms
be a discrete random
variable with a finite number of atoms ![]() , where
, where ![]() . Moreover, let
one of the following two conditions be fulfilled:
. Moreover, let
one of the following two conditions be fulfilled:
Then the sequence ![]() for some
for some ![]()
![]() if
if ![]() and
and
![]() if
if ![]() ,
where
,
where ![]()
![]()
![]() does not satisfy
does not satisfy ![]() -mixing.
-mixing.
Theorem 1. Let ![]() be a bounded nondegenerated
random variable and the set
be a bounded nondegenerated
random variable and the set ![]() be infinite.
Then the sequence
be infinite.
Then the sequence
![]() does not satisfy
does not satisfy ![]() -mixing.
-mixing.
Theorem 2.
Let
the following conditions be fulfilled:
Then the sequence ![]() ,
, ![]() ,
, ![]()

![]() ;
;
![]() .
.![]() does not satisfy
does not satisfy ![]() -mixing.
-mixing.
Vladimir Vatutin![]()
Steklov Mathematical Institute of RAS, Moscow, Russia
A continuous time branching random walk on the lattice ![]() is considered in which individuals may produce children at the origin
only. Each individual spends at the origin an exponentially distributed
time with parameter 1 and then either jumps to a point
is considered in which individuals may produce children at the origin
only. Each individual spends at the origin an exponentially distributed
time with parameter 1 and then either jumps to a point ![]() with
probability
with
probability ![]() , or dies with probability
, or dies with probability ![]() producing just before the death a random number of
children
producing just before the death a random number of
children ![]() . Individuals outside the origin perform a Markov
random walk without reproduction, i.e., an individual spends in a
state
. Individuals outside the origin perform a Markov
random walk without reproduction, i.e., an individual spends in a
state ![]() an exponential time with parameter
an exponential time with parameter ![]() and then
jumps to a point
and then
jumps to a point ![]() with probability
with probability
Let ![]() and
and ![]() be the numbers of individuals at
the origin and outside the origin at moment
be the numbers of individuals at
the origin and outside the origin at moment ![]() respectively.
Assuming that the underlying Markov random walk is homogeneous and
symmetric, and the reproduction law of
respectively.
Assuming that the underlying Markov random walk is homogeneous and
symmetric, and the reproduction law of ![]() is critical, we
describe the asymptotic behavior, as
is critical, we
describe the asymptotic behavior, as ![]() of
the conditional distribution of the two-dimensional vector
of
the conditional distribution of the two-dimensional vector ![]() (scaled in an appropriate way), given
(scaled in an appropriate way), given ![]() .
.
The case ![]() has been investigated by the authors in
has been investigated by the authors in
Individuals at the origin in the critical catalytic branching random
walk. Discrete Mathematics ![]() Theretical Computer Science (electronic),
v.6 (2003), 325-332.
Theretical Computer Science (electronic),
v.6 (2003), 325-332.
http://dmtcs.loria.fr/proceedings/html/dmAC7130.abs.html
Two-dimensional limit theorem for a critical catalytic branching random walk. In Mathematics and Computer Science III, Algoritms, Trees, Combinatorics and Probabilities, Editors M.Drmota, P.Flajolet, D.Gardy, B.Gittenberger. Birkhauser, Verlag, Basel-Boston-Berlin, (2004), 387-395.
Limit Theorem for Critical Catalytic Branching Random Walks. Theory of Probability & Its Applications, V.49 (2005), no. 3. pp. 498-518.
![]() Supported by grants: RFBR-NWO 047.016.013, RFBR 06-01-00127, Russian Scientific School 4129.2006.1
Supported by grants: RFBR-NWO 047.016.013, RFBR 06-01-00127, Russian Scientific School 4129.2006.1
![]() Supported by grants: RFBR-NWO 047.016.013, RFBR 05-01-00035, Russian Scientific School 4129.2006.1
Supported by grants: RFBR-NWO 047.016.013, RFBR 05-01-00035, Russian Scientific School 4129.2006.1
Institute of Applied Mathematics, Far Eastern Branch of RAS, Vladivostok, Russia
In this paper new product theorems for opened queueing networks with unreliable elements: nodes, links between nodes and servers in nodes are proved. Limit distributions calculations are based on different schemes of elements recovery (independent recovery, recovery with one repair place and restoration network scheme), routing algorithms and service disciplines. Thus an introduction of special control allows to connect queueing networks theory with reliability theory. Obtained results may be spread onto closed queueing networks practically without changes.
![]() Partially supported by RFBR, project 06-01-00063-à and FEB RAS,
project 06-III-A-01-016
Partially supported by RFBR, project 06-01-00063-à and FEB RAS,
project 06-III-A-01-016
Moscow State University, Moscow, Russia
Joint work with Gerd Christoph (Magdeburg, Germany)
and Yasunori Fujikoshi (Tokyo, Japan)
Put
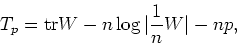
Let ![]() be the distribution function of chi-squared random
variable with
be the distribution function of chi-squared random
variable with ![]() degrees of freedom.
degrees of freedom.
We prove that
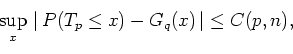
The possible extensions of the result are discussed.
Steklov Mathematical Institute, Moscow, Russia
First models of branching processes were investigated in the 80th of 19th century by two British scientists - Galton and Watson in connection with the study of extinction of nobel families. Now, owing to the efforts of Kolmogorov, Sevastuanov, Bellman, Harris, Athreya, Ney, Dawson, Dynkin and many others the theory of branching processes becomes one of the important parts of probability theory . Many results of this theory occur to be useful in various fields of science from physics and chemistry to biology. However, the classical models of branching processes do not reflect phenomena essential to the evolution of populations one of the most important of which is oscillation of the number of individuals (and not permanent exponential growth or rapid extinction as is usual in the classical models).
In our talk we consider a model of branching processes in random environment where oscillation of the size of populations is an essential feature. In particular, we formulate mathematical results which show (at least in the framework of the model under consideration and at the theoretical level) that the evolution of a population consists of favorable and unfavorable stages. Unfavorable periods reduce the size of the population to a finite (bounded) number of individuals. These periods are followed by favorable time-intervals when the population ``recovers' and rapidly reestablishes its size. In real populations such phenomena is called the bottleneck of evolution of populations.
Universidade da Beira Interior, Covilhã, Portugal
This communication is based on joint work with J.M.R. Gama. It
considers some properties of wavelet density estimators (WDE)
that reconstruct a density ![]() from i.i.d.
observations
from i.i.d.
observations ![]() with this density. A WDE is essentially
a partial sum of the multiresolution expansion based on a
sequence of scales
with this density. A WDE is essentially
a partial sum of the multiresolution expansion based on a
sequence of scales ![]() ,
,
 | (1) |
For the so-called linear WDE ![]() , which changes
coefficients
, which changes
coefficients ![]() to sample means, the squared
to sample means, the squared ![]() -norm
-norm
![]() of the random component of its error proves
asymptotically normal [1] if the number
of the random component of its error proves
asymptotically normal [1] if the number
![]() of "detail layers" retained goes to
infinity with sample size:
of "detail layers" retained goes to
infinity with sample size:
![]() , and the distribution of
, and the distribution of ![]() weakly
converges to the standard normal law on
weakly
converges to the standard normal law on ![]() .
.
A "thresholded" WDE ![]() is obtained from a linear
one by suppression of less relevant terms. The efficiency of
these non-linear WDE's was studied predominantly in terms of
integral risks. Yet, a thresholded WDE admits an exponential
inequality, resembling (at least in form) that of S.N.Bernstein,
is obtained from a linear
one by suppression of less relevant terms. The efficiency of
these non-linear WDE's was studied predominantly in terms of
integral risks. Yet, a thresholded WDE admits an exponential
inequality, resembling (at least in form) that of S.N.Bernstein,
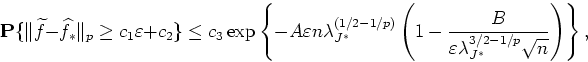
![]() Work supported by Fundação para a
Ciência e a Tecnologia (Portugal) through Centro de
Matem'atica da Universidade da Beira Interior,
Sub-Projecto DECONT.
Work supported by Fundação para a
Ciência e a Tecnologia (Portugal) through Centro de
Matem'atica da Universidade da Beira Interior,
Sub-Projecto DECONT.
St. Petersburg Department of Steklov Mathematical Institute,
St.Petersburg, Russia
Let ![]() be an even positive
function such that
be an even positive
function such that ![]() and the function
and the function ![]() is non-decreasing.
is non-decreasing.
Theorem 1. Suppose that ![]() are independent random vectors with
are independent random vectors with ![]() ,
, ![]() . Let
. Let
![]() and
and ![]() .
Write
.
Write
![]() ,
where
,
where ![]() denote the inverse function for
denote the inverse function for ![]() Assume that there exists a
strictly increasing sequence of non-negative integers
Assume that there exists a
strictly increasing sequence of non-negative integers ![]() ,
, ![]() satisfying the
following conditions. Let
satisfying the
following conditions. Let
![]() ,
,![]() ,
, ![]() ,and assume that for all
,and assume that for all ![]() , and
, and ![]() ,
,
![]()
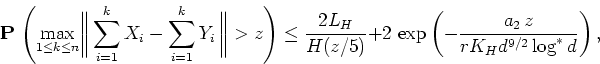
Theorem 1 is a consequence of the result of the author [2] and can be considered as
multidimensional generalization of a weakened version of a result of
Sakhanenko [1].
The conditions of Theorem 1 are satisfied, for example, for the functions ![]() ,
,![]() , with
, with ![]() .
.
![]() Research
partially supported by Russian Foundation of Basic Research (RFBR) Grant
05-01-00911, by RFBR-DFG Grant 04-01-04000, and by INTAS Grant 03-51-5018.
Research
partially supported by Russian Foundation of Basic Research (RFBR) Grant
05-01-00911, by RFBR-DFG Grant 04-01-04000, and by INTAS Grant 03-51-5018.
Statistics and Modelling Science dept., University of Strathclyde
Joint work with Yury Davydov and Ilya Molchanov
Notion of a stable distribution is one of central in the Theory of
Probability. It naturally appears in the Central Limit Theorem (CLT) for
random vectors (and generally, random elements in a Banach space ![]() ) and
characterised by the parameter
) and
characterised by the parameter ![]() .
The case
.
The case ![]() corresponds to
the classical Gaussian CLT, while stable distributions with
corresponds to
the classical Gaussian CLT, while stable distributions with ![]() arise when the second and/or the first moment of the summands does not exist. The
symmetric alpha-stable random elements can be represented as a sum of points
of a Poisson process known as the LePage representation. This point process
is union-stable, i.e. the union of its two independent copies coincides in
distribution with the rescaled original point process. This shows that the
classical definition of stable random elements is closely related to the
union-stability property of point processes.
arise when the second and/or the first moment of the summands does not exist. The
symmetric alpha-stable random elements can be represented as a sum of points
of a Poisson process known as the LePage representation. This point process
is union-stable, i.e. the union of its two independent copies coincides in
distribution with the rescaled original point process. This shows that the
classical definition of stable random elements is closely related to the
union-stability property of point processes.
These concepts make sense in any convex cone ![]() , i.e. in a semigroup equipped
with multiplication by numbers, and lead to a construction of stable laws in
general cones by means of the LePage series. Examples include compact sets
with union operation, measures with convolution or with superposition
operation, positive numbers with harmonic mean operation etc. We establish
limit theorems for normalised sums of random elements with
, i.e. in a semigroup equipped
with multiplication by numbers, and lead to a construction of stable laws in
general cones by means of the LePage series. Examples include compact sets
with union operation, measures with convolution or with superposition
operation, positive numbers with harmonic mean operation etc. We establish
limit theorems for normalised sums of random elements with
![]() -stable limit for
-stable limit for ![]() and deduce the LePage representation for
strictly stable random vectors in these general cones.
and deduce the LePage representation for
strictly stable random vectors in these general cones.
By using the technique of harmonic analysis on semigroups we characterise
distributions of ![]() -stable random elements and show how possible values
of the characteristic exponent
-stable random elements and show how possible values
of the characteristic exponent ![]() relate to the properties of the
semigroup and the corresponding scaling operation, in particular, their
distributivity properties.
relate to the properties of the
semigroup and the corresponding scaling operation, in particular, their
distributivity properties.
 Return to
Conference Home Page
Return to
Conference Home Page