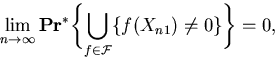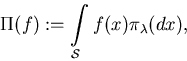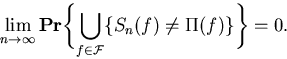Let ![]() be an arbitrary measurable space.
Denote by
be an arbitrary measurable space.
Denote by ![]() the minimal
the minimal
![]() -field
generated by the standard product
-field
generated by the standard product ![]() -field
-field ![]() and diagonal
and diagonal ![]() of the product space.
of the product space.
Denote by ![]() the total variation distance between
distributions
of random variables X and Y taking values in
the total variation distance between
distributions
of random variables X and Y taking values in ![]() .We discuss the following generalization of the fundamental result proved
independently by R.M.Dudley (for Polish spaces, 1968) and by
R.L. Dobrushin (for separable metric spaces, 1970).
.We discuss the following generalization of the fundamental result proved
independently by R.M.Dudley (for Polish spaces, 1968) and by
R.L. Dobrushin (for separable metric spaces, 1970).
Theorem 1. On the probability space ![]() ,one can construct copies X0 and Y0 of arbitrary random variables X and Y
in
,one can construct copies X0 and Y0 of arbitrary random variables X and Y
in ![]() such that
such that
![]()
and, moreover,
where the infimum in (2) is taken over all pairs
(X, Y) based on the above probability space and having
initial marginal distributions.
Let ![]() be row-wise i.i.d.r.v-s in
be row-wise i.i.d.r.v-s in
![]() For each n, introduce the normalized empirical process
based on the sample
For each n, introduce the normalized empirical process
based on the sample ![]() and indexed by a family
and indexed by a family
![]() of real-valued Borel measurable functions on
of real-valued Borel measurable functions on
![]()
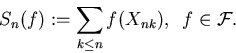
Theorem 2. Let ![]() be a finite measure on
be a finite measure on ![]() such that
such that ![]() as
as ![]() If,
additionally,
If,
additionally,