Large Deviations in Boundary-valued Problems
for One-dimensional Markov Chains
Borovkov, Alexandr (Novosibirsk, Russia)
borovkov@math.nsc.ru
Let 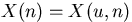 ,
, 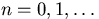 -- be a
homogeneous in time ergodic Markov Chain on the real line.
-- be a
homogeneous in time ergodic Markov Chain on the real line.
The main goal of the paper is to study large deviations problems
on asymptotics of
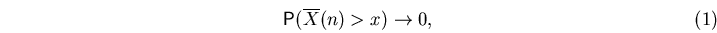
where
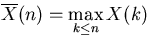 ,
,
and a more
general boundary-valued problem on asymptotics of
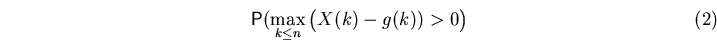
for a given arbitrary sequence 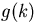 ,
, 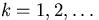 .
.
![]() ,
, ![]() -- be a
homogeneous in time ergodic Markov Chain on the real line.
-- be a
homogeneous in time ergodic Markov Chain on the real line.
![]()
![]() ,
,
![]()