Large Deviations for Partially Homogeneous Markov Chains
in
Positive Quadrant
Mogulskii, Anatolii (Novosibirsk, Russia)
mogul@math.nsc.ru
(joint work with Akeksandr Borovkov)
In the talk so-called
N -partially homogeneous (in space)
Markov chains 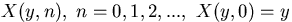 , in
positive quadrant
, in
positive quadrant 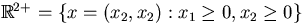 , are considered. These chains are characterized
by the property of the transition probability
, are considered. These chains are characterized
by the property of the transition probability
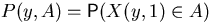 :
:
- for some
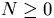 the measure P(y,dx)
in the domain
the measure P(y,dx)
in the domain 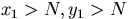 depends on x2, y2, x1-y1 only,
and in the domain
depends on x2, y2, x1-y1 only,
and in the domain 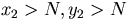 -- on x1, y1, x2-y2 only.
-- on x1, y1, x2-y2 only.
For such chains the so-called integro-local large deviations principle has been
obtained:
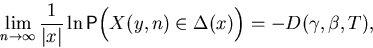
where 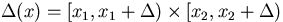 ,
, 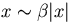 ,
, 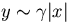 ,
, 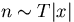 and the rate function
and the rate function
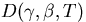 is known in explicit form.
For ergodic Markov chains
the precise asymptotic of the probabilities
is known in explicit form.
For ergodic Markov chains
the precise asymptotic of the probabilities
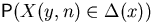 have been found.
have been found.
![]() , in
positive quadrant
, in
positive quadrant ![]() , are considered. These chains are characterized
by the property of the transition probability
, are considered. These chains are characterized
by the property of the transition probability
![]() :
:
![]()