Convergence Conditions for Weighted Branching Processes¹

Rösler, Uwe (Kiel, Germany),
roesler@math.uni-kiel.de
Topchii, Valentin (Omsk, Russia),
topchij@iitam.omsk.net.ru
Vatutin, Vladimir (Moscow)
vatutin@mi.ras.ru

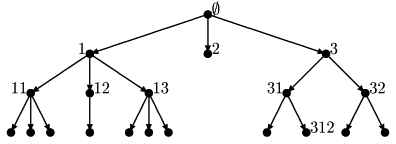
A weighted branching process is a branching process with an additional weight L(v) of the individual v . The weight L(vi) of the child vi is the weight L(v) of the mother v multiplied by a random factor T_i(v) . A handy description of this process is via a (Markov) process on a directed tree with countable many branches. The following picture shows a realisation on the tree of all living (= weight $L(v)\ne0$) individuals v indexed by the path.

$\parbox{10cm}{\quad \begin{center} \unitlength1cm \begin{picture} (10... ...13} \put(6.5,1){31} \put(9.1,1){32} \put(7.6,0){312}\end{picture}\end{center} }$

A major and well studied example are Galton-Watson processes, where the weight of each individual is either or 1 . However many methods, especially the essential tool of generating functions, will not work for the weighted branching process. We consider some aspects of the weighted branching processes and, in particular, consider convergence conditions for the processes being a certain analogue of the well-known $X\ln X$ condition for ordinary branching processes and branching random walks on $\mathbb R$.