Solution of Monge-Kantorovich Problem for a Certain Class
of Functionals and Application to Poisson Approximation
Rouzankin, Pavel (Novosibirsk, Russia)
ruzankin@math.nsc.ru
Let P and Q be Borel probability measures on the real line.
Consider the functional
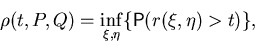 where infimum is taken over all random variables
where infimum is taken over all random variables 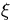 and
and 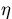 defined on a common probability space with distributions P and Q ,
respectively.
R.M. Dudley proved (1968) that
defined on a common probability space with distributions P and Q ,
respectively.
R.M. Dudley proved (1968) that
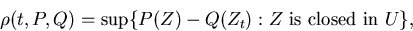
where 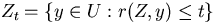 . The main goal of the talk is to give some more convenient
representation for the functional
. The main goal of the talk is to give some more convenient
representation for the functional 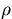 .
Denote by F and G the distribution functions for
P and Q , respectively. Then
.
Denote by F and G the distribution functions for
P and Q , respectively. Then
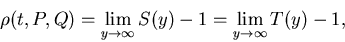
where functions S and T are defined by the requirement of left-continuity
and by the relations:
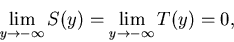
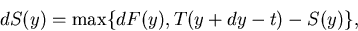
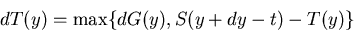
for all y .
The functions S and T meeting the conditions above always exist
and are uniquely defined.
The result is applied to estimate distance 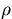 between binomial
distribution and Poisson distribution.
between binomial
distribution and Poisson distribution.
![]() where infimum is taken over all random variables
where infimum is taken over all random variables ![]() and
and ![]() defined on a common probability space with distributions P and Q ,
respectively.
R.M. Dudley proved (1968) that
defined on a common probability space with distributions P and Q ,
respectively.
R.M. Dudley proved (1968) that
![]()
![]()
![]()
![]()
![]()
![]() between binomial
distribution and Poisson distribution.
between binomial
distribution and Poisson distribution.