Long Time Dynamics in Large Jackson Networks

Scherbakov, Vadim (Moscow, Russia)
scherbak@mtu-net.ru

Non-equilibrium dynamics of symmetrical closed Jackson networks is studied here.

We assume thermodynamic limit condition for considered Jackson networks. It means that M - the number of particles and N - the number of nodes tend to infinity in such way that there exists the limiting particle density: $$\frac{M}{N} \rightarrow \lambda.$$ We study the dynamics of the system on linear in N times.

Non-trivial dynamics of closed Jackson network arises at this time scale when an initial condition is far from the equilibrium. It is the case when there are linear in N queues.

We consider the sequence of symmetrical closed Jackson networks J_N, consisting of N exponential servers with service rates 1 and irreducible routing matrix $R=\{r_{ij,N=\frac{1}{N}}\}$and M_N particles circulating in the network J_N. Recall that this means that a particle in the queue at node i waits until all particles ahead have been served, and then receives service whose duration is an exponential random variable with mean 1, all service times being independent. A particle finishing service at node i is routed to node j with probability 1/N, all routing decisions being independent and independent of the service times.

We shall assume the following condition

• Thermodynamics limit condition:
  N and M_N go to infinity in such way that

  $$\frac{M_{N}}{N}=\lambda_{N} \rightarrow \lambda \gt 0$$

  For simplicity of notation we assume in the sequel that $\lambda_{N}=\lambda$ for all N.

Let $\eta_{i}(t)$ be the queue length in the node i at the time t. Let us introduce the following random process:

$$\vec{\zeta}^{(N)}(tN)=\vec{\xi}^{(N)}(tN)N^{-1}$$

where

$$\vec{\xi}^{(N)}(s)=\{\xi^{(N)}_{k}(s), k\geq 0\}$$

$\xi_{k}^{(N)}(s)=\char93 \{i\in \{2,\ldots,N\}:\eta_{i}(s)=k\}$ - is the number of nodes $i,\, i\geq 2$ with k particles at the time s .

Let $\nu(tN)$ be the distribution of the process $\vec{\xi}^{(N)}(tN)N^{-1}$.

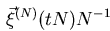Theorem 1.

 Let us suppose that the sequence of initial states of the networks J_N is the following

$$\eta_{1}^{(N)}(0) = M_{N}, \eta_{i}^{(N)}(0) = 0, i= 2,3,...,N$$

Then the sequence of probability measures $\nu(tN)$converges weakly to the measure concentrated in the point $\vec{\pi}_{\lambda(t)}=\{\pi_{\lambda(t),k} =\frac{\lambda^{k}(t)}{(1+\lambda(t))^{k+1}},\,k\geq 0 \}$, the function $\lambda(\cdot)$ is defined as follows  

$$\lambda(t) = \sqrt{2t+1} - 1,\,\, \mbox{if} \,\, t\leq t_{cr}$$

$$\lambda(t) = \lambda,\,\,\mbox{if}\,\, t \gt t_{cr}$$

$$t_{cr} = \frac{(1+\lambda)^{2} - 1}{2}$$