Localization of Spectum Bottom of the Stokes Operator
in Random Porous Medium

Yurinsky, Vadim (Covilhã, Portugal)
yurinsky@ubi.pt

This communication is dedicated to asymptotic behavior of the spectrum bottom of the Stokes operator acting on solenoidal functions over a random domain which is the part occupied by pores in a large regular region in $\mathbb {R} ^{d}$. The problem arises naturally in the study of flows of incompressible constant-density fluids in disordered porous media -- in this setting the lowest eigenvalue determines an essential time scale of the Stokes flow.

The flow domain considered is $rQ\backslash P$, where P is the random ``hard skeleton'' of the porous medium and $rQ=\left( -\frac{1}{2}r,\frac{1}{2}r\right) ^{d}$. A typical choice of P is the union of translates of a regular closed bounded ``standard obstacle'' $W\subset \mathbb {R} ^{d}$ by points of a spatial Poisson point process with constant intensity $\nu$. The smallest eigenvalue of the Stokes system is $\mathfrak {s} _{r}=1/ \mathfrak {S} _{r}$,where

$$\mathfrak {S} _{r}=\inf\left\{ \lambda\in \mathbb {R} :\fora... ...\vert \nabla\otimes u\left( x\right) \right\vert ^{2}dx\right\}$$

(the inequality in the definition is supposed to hold for all functions $u: \mathbb {R} ^{d}\rightarrow \mathbb {R} ^{d}$ which have zero divergence and vanish outside $Q_{N}\backslash P$). The asymptotic behavior of the random variable $\mathfrak {s} _{r}$ is analyzed for $r\rightarrow\infty$.

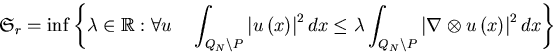
In the case of the Laplacian acting on scalar functions, it was earlier established that the smallest eigenvalue $\lambda\left( r\right)$ behaves as $\lambda_{1}\left( \frac{\nu}{d}\ln r\right) ^{-2/d}$, where $\lambda _{1}$ is the smallest ``Dirchlet'' eigenvalue of the Laplacian in the ball of unit volume (see [1] and [2] on confidence bounds for $\lambda\left( r\right)$). The present communication shows that the smallest Stokes eigenvalue $\mathfrak {s} _{r}$ is asymptotically equivalent to $\mathcal{S}^{-1}\left( \frac{\nu}{d}\ln r\right) ^{2/d}$, where $\mathcal{S}$ is the maximal Rayleigh ratio for solenoidal functions on $\mathbb {R} ^{d}$ whose support has unit Lebesgue measure. The method is a modification of one in [3]. The result is less exact due to additional difficulties caused by the restriction of the class of test functions u to that of solenoidal ones.

References

1

Sznitman A.-S. Fluctuation of principal eigenvalues and random scales. Commun. Math. Phys. , 1997, v.189, 337-363.

2

Yurinsky V. V. Spectrum bottom and largest vacuity. Probab. Theory Relat. Fields , 1999, v.114, 151-175.

3

Yurinsky V.V. Raising spectrum bottom by random potential. Siberian Adv. Math. , 1997, v.7, No 2, 124-150.