С.Л. Соболев

 

Сергей Львович Соболев

(1908-1989)

 

 

    English


Материалы о С.Л. Соболеве

Сергей Львович Соболев родился 6 октября 1908 года в г. Петербурге. Его отец, Лев Александрович, был юристом, участвовал в революционном движении, за что исключался из Петербургского университета. Мать, Наталья Георгиевна, также в молодости была революционеркой, членом РСДРП. Она преподавала в частной гимназии литературу и историю, в дальнейшем окончила медицинский институт, работала доцентом Ленинградского медицинского института. Сергей Львович рано потерял отца, его воспитывала мать, которая привила Сергею Львовичу честность, принципиальность и целеустремленность.

С.Л. СоболевС детства Сергей Львович отличался большой любознательностью, много читал, увлекался математикой, физикой, философией, биологией, медициной, писал стихи, учился игре на фортепьяно. После окончания школы в 1924 году Сергей Львович из-за «малолетства» не мог поступать в ВУЗ. В то время принимали с 17 лет по путевкам, полученным родителями на работе. Поэтому в 1924 году Сергей Львович поступил в Первую государственную художественную студию по классу фортепьяно. Через год он стал студентом физико-математического факультета Ленинградского государственного университета, одновременно продолжая заниматься в художественной студии. Ленинградский университет был крупнейшим математическим центром, сохранившим замечательные традиции Петербургской математической школы, знаменитой своими величайшими открытиями и связанной с именами П.Л. Чебышёва, А.Н. Коркина, А.М. Ляпунова, А.А. Маркова, В.А. Стеклова и др. 

Во время обучения в Ленинградском университете С.Л. Соболев слушал лекции профессоров Н.М. Гюнтера, В.И. Смирнова, Г.М. Фихтенгольца, оказавших большое влияние на формирование С.Л. Соболева, как ученого. Под руководством Н.М. Гюнтера С.Л. Соболев написал дипломную работу об аналитических решениях системы дифференциальных уравнений с двумя независимыми переменными, которая была опубликована в Докладах академии наук СССР. В 1929 году после окончания университета С.Л. Соболев был принят на работу в теоретический отдел Сейсмологического института АН СССР, который возглавлял В.И. Смирнов. За время работы в Сейсмологическом институте С.Л. Соболев выполнил ряд глубоких научных исследований. Совместно с В.И. Смирновым он разработал метод функционально-инвариантных решений, который затем был применен к решению ряда динамических задач теории упругости. На основе этого метода была построена теория распространения упругих волн. В частности, решена знаменитая задача Лэмба о нахождении смещения упругой полуплоскости под действием сосредоточенного импульса, построена строгая теория поверхностных волн Релея, решена задача дифракции упругих волн вблизи сферической поверхности, проведены исследования распространения сильных разрывов в задачах упругости. С.А. Чаплыгин, С.Л. Соболев, А.Н. Крылов

Результаты по динамическим задачам теории упругости подробно изложены С.Л. Соболевым в двенадцатой главе «Некоторые вопросы теории распространения колебаний» второй части книги Ф. Франка, Р. Мизеса «Дифференциальные и интегральные уравнения математической физики» (1937). Эти результаты используются в современных математических методах разведки полезных ископаемых, в обратных задачах сейсмики, при изучении трещин в упругой среде. 

Прикладные задачи, связанные с распространением волн в упругих средах, требовали новых подходов к изучению уравнений с частными производными. В этот период С.Л. Соболев начинает изучение задачи Коши для гиперболических уравнений с переменными коэффициентами. В 1930 году на I Всесоюзном математическом съезде в г. Харькове С.Л. Соболев делает доклад «Волновое уравнение в неоднородной среде», в котором он предлагает новый метод решения задачи Коши для волнового уравнения с переменными коэффициентами. Присутствовавший на съезде известный французский математик Ж. Адамар сказал С.Л. Соболеву: «Я буду очень рад, молодой коллега, если Вы будете держать меня в курсе Ваших дальнейших работ, чрезвычайно меня заинтересовавших». 

С 1932 года С.Л. Соболев начинает работать в отделе дифференциальных уравнений Математического института им. В.А. Стеклова, а через год за выдающиеся заслуги в математике он избирается членом-корреспондентом Академии наук СССР. С 1934 года начинается «московский период» деятельности С.Л. Соболева, вместе с Математическим институтом им. В.А. Стеклова он переезжает в г. Москву и назначается заведующим отделом. В это время С.Л. Соболев получает фундаментальные результаты в теории уравнений с частными производными и функциональном анализе, которые вошли в золотой фонд мировой математики. Идеи и методы, предложенные в этих работах, развивались в дальнейшем в трудах многих математиков в нашей стране и за рубежом.

С.Л. СоболевИзучение задачи Коши для гиперболических уравнений и разрывных решений уравнений теории упругости привело С.Л. Соболева к понятию обобщенного решения дифференциального уравнения, играющему фундаментальную роль в современной теории уравнений с частными производными. В 1934 году на II Всесоюзном математическом съезде в г. Ленинграде С.Л. Соболев делает три доклада по теории уравнений с частными производными, касающихся задач теории упругости и задачи Коши для гиперболических уравнений. Название одного из докладов – «Обобщенные решения волнового уравнения». Так было положено начало теории обобщенных функций. В 1935-36 годах С.Л. Соболев дает развернутое изложение результатов, представленных в этих докладах, в двух знаменитых работах «Общая теория дифракции волн на римановых поверхностях» и «Новый метод решения задачи Коши для линейных нормальных гиперболических уравнений». В этих работах впервые подробно излагаются основы теории обобщенных функций.  

Возникновение теории обобщенных функций было подготовлено развитием математического анализа и теоретической физики. Известные идеи Хевисайда, Дирака, Кирхгофа и Адамара способствовали ее появлению. Однако в работах предшественников не было понятий и построений, подобных строгим конструкциям С.Л. Соболева. Следует отметить, что для С.Л. Соболева обобщенные функции были прежде всего аппаратом, важным для приложений. 

В последующие годы С.Л. Соболев развивает теорию обобщенных функций в новом направлении. На основе понятия обобщенной производной он вводит и изучает новые функциональные пространства, которые в литературе стали называть соболевскими пространствами. Для этих пространств С.Л. Соболев доказывает первые теоремы вложения, он применяет эти пространства при исследовании краевых задач для эллиптических уравнений высокого порядка. В 1939 году была опубликована статья С.Л. Соболева «К теории нелинейных гиперболических уравнений с частными производными», в которой он использует развитую им теорию пространств и решает задачу Коши для квазилинейных гиперболических уравнений второго порядка. 

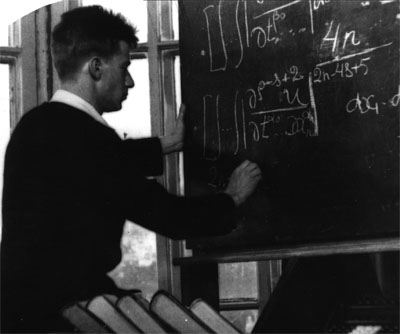С.Л. СоболевСистематическое изложение теории функциональных пространств, теорем вложений этих пространств, теорем о следах и приложений этих результатов к задачам дифференциальных уравнений в частных производных и уравнений математической физики содержится в знаменитой книге С.Л. Соболева «Некоторые применения функционального анализа в математической физике» (1950). Эта книга стала настольной не только для математиков, но и для представителей многих других наук. Она трижды переиздавалась в нашей стране, дважды в США, переведена на многие языки мира. Понятия обобщенной производной и обобщенного решения приобрели широчайшее распространение, в математике сформировалось новое направление исследований, получившее название «теория пространств Соболева». С.Л. Соболев не только заложил основы теории обобщенных функций и теории новых функциональных пространств, но и показал их практическое применение при изучении краевых задач для дифференциальных уравнений. 

Идеи и методы С.Л. Соболева получили широкое развитие и приложения в дифференциальных уравнениях, уравнениях математической физики и вычислительной математике. А теоремы вложения и теоремы о следах стали одним из важнейших средств современного математического анализа. 

В 1939 году за выдающиеся математические открытия С.Л. Соболев был избран действительным членом Академии наук СССР, долгое время оставаясь самым молодым академиком в стране. По воспоминаниям его жены А.Д. Соболевой: «Сергей Львович постоянно твердил, что он должник АН СССР и когда-нибудь постарается оправдать звание академика». Много лет спустя в беседе с журналистами С.Л. Соболев говорил: «Что касается моих работ, то тогда никто еще не мог разобраться, что из этого вырастет, выбран в Академию я был в кредит». 

С.Л. СоболевВ 1941 году в самом начале Великой отечественной войны на академика С.Л. Соболева были возложены обязанности директора Математического института им. В.А. Стеклова. В трудных условиях эвакуации в г. Казани Сергей Львович многое сделал для организации в Математическом институте прикладных исследований и оказания эффективной помощи фронту. В 1943 году после возвращения Математического института в г. Москву С.Л. Соболев переходит на работу в Лабораторию № 2 (ЛИПАН), возглавляемую академиком И.В. Курчатовым (впоследствии эта лаборатория была преобразована в Институт атомной энергии). С.Л. Соболев назначается первым заместителем директора и председателем Ученого совета. С этого момента фамилия С.Л. Соболева надолго исчезает со страниц газет. 

В лаборатории в обстановке глубокой секретности велись интенсивные работы по созданию атомного щита страны, это был период напряженной творческой работы коллектива ученых института над созданием новой техники. С.Л. Соболев работал вместе с физиками, академиками И.В. Курчатовым, И.К. Кикоиным, М.А. Леонтовичем и др. Нужно было понимание всего физического процесса в целом, требовалось решать крупные конкретные задачи при очень малых вычислительных средствах. Перед С.Л. Соболевым были поставлены математические прикладные задачи, которые требовали больших усилий, так как рассчитывать, оптимизировать, предсказывать приходилось сложнейшие процессы, которые никогда до этого не изучались. Нужны были необыкновенная математическая интуиция и огромный труд, чтобы исчерпывающе и в заданный срок решать очень сложные конкретные задачи. Жена Ариадна Дмитриевна Соболева вспоминает: «В период работы в Институте атомной энергии он месяцами не бывал дома, часто уезжал в длительные и далекие командировки». В этот период за исключительные заслуги перед государством академик С.Л. Соболев был отмечен двумя Государственными премиями и званием Героя Социалистического Труда. 

В пятидесятые годы С.Л. Соболев издает свою знаменитую книгу «Некоторые применения функционального анализа в математической физике» (1950), пишет ряд фундаментальных работ по уравнениям с частными производными, функциональному анализу и вычислительной математике. В частности, выходит в свет его знаменитая статья «Об одной новой задаче математической физики» (1954), положившая начало систематическим исследованиям новых классов уравнений и систем, не разрешенных относительно старшей производной. В настоящее время в литературе такие уравнения называются уравнениями соболевского типа. Эта проблематика возникла в связи с задачами о движении вращающейся жидкости (1943). За эти работы С.Л. Соболеву была присуждена Государственная премия (1986). 

В пятидесятые годы С.Л. Соболев также много внимания уделяет вопросам вычислительной математики. В частности, он разрабатывает понятие замыкания вычислительного алгоритма, исследует дискретные задачи, возникающие при аппроксимации дифференциальных и интегральных уравнений. С.Л. Соболев рассказывает: «Работая в Институте атомной энергии, я приобрел вкус к вычислительной математике, осознал ее исключительные возможности. Поэтому я с удовольствием принял предложение И.Г. Петровского возглавить первую в нашей стране кафедру вычислительной математики Московского университета». С.Л. Соболев заведовал кафедрой с 1952 по 1958 годы. В эти годы он вместе с А.А. Ляпуновым активно выступал в защиту кибернетики, доказывая ее важное предназначение. 

С.Л. Соболев на стройплощадке Института математики

В 1956 году академики М.А. Лаврентьев, С.Л. Соболев, С.А. Христианович выступили с предложением разработать план мероприятий по созданию научных центров на востоке нашей страны. В 1957 году было принято решение о создании Сибирского отделения Академии наук СССР в составе нескольких научно-исследовательских институтов, в числе которых был Институт математики. Академик С.Л. Соболев был назначен директором этого Института. С 1958 года начинается «сибирский период» деятельности С.Л. Соболева. Укомплектовав за год в г. Москве несколько отделов будущего Института математики, вместе со своими сотрудниками он переезжает на постоянную работу в г. Новосибирск. «Многие не понимали, даже друзья, что собственно заставило меня, - говорит Сергей Львович, - покинуть сильную кафедру в Московском университете и ехать в Сибирь, которая была по существу научной целиной». Ответ самого С.Л. Соболева на этот вопрос, как всегда, чрезвычайно скромен: «Естественное желание человека прожить несколько жизней, начать что-то новое». 

Возглавляя Институт математики, С.Л. Соболев стремился к тому, чтобы в Институте были представлены все важнейшие направления современной науки. Направление по алгебре и логике в Институте успешно развивалось под руководством академика А.И. Мальцева, исследования по геометрии проводились под руководством академика А.Д. Александрова. Математико-экономический отдел возглавил академик Л.В. Канторович, отдел вычислительной математики – академик Г.И. Марчук, отдел теоретической кибернетики – член-корр. АН СССР А.А. Ляпунов. Исследования по дифференциальным уравнениям и функциональному анализу проводились под руководством академика С.Л. Соболева. В работе по организации Института большую помощь С.Л. Соболеву оказывал его заместитель член-корр. АН СССР А.И. Ширшов. В кратчайшие сроки Институт математики стал всемирно известным математическим центром. 

С.Л. Соболев

С.Л. Соболев является одним из основателей Новосибирского государственного университета. Именно он прочитал в НГУ первую лекцию по математике. С.Л. Соболев заведовал кафедрой дифференциальных уравнений, читал курс по уравнениям математической физики и спецкурс по кубатурным формулам, руководил работой спецсеминаров. 

В «сибирский период» С.Л. Соболев начинает исследования по новой теме – кубатурные формулы. С.Л. Соболев рассказывает: «После переезда из Москвы в Новосибирск мои мысли занимают кубатурные формулы. Случилось так, что они заставили меня вернуться к классическим работам Эйлера. Мне пришлось исследовать некоторые свойства многочленов Эйлера, которые не были известны великому классику математики. Это было возвращением к истокам». 

Задача о приближенном интегрировании функций является одной из основных задач теории вычислений. Она чрезвычайно трудоемка в вычислительном плане для многомерных интегралов. В результате исследований новых задач функционального анализа, уравнений с частными производными, теории функций, ориентированных на решение проблем вычислительной математики, С.Л. Соболев создает теорию кубатурных формул. В г. Новосибирске С.Л. Соболев написал фундаментальную монографию «Введение в теорию кубатурных формул», изданную в 1974 году. Эта книга подвела итог многолетним исследованиям автора по кубатурным формулам.

В 1983 году закончился «сибирский период» деятельности С.Л. Соболева, в 1984 году он возвращается в г. Москву и продолжает работать в Математическом институте им. В.А. Стеклова в отделе академика С.М. Никольского. 

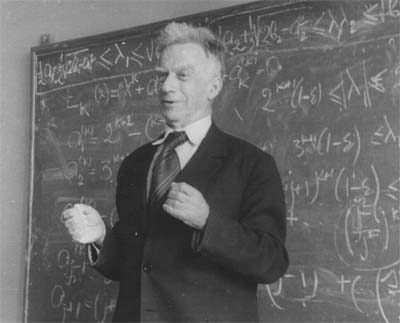С.Л. СоболевВыдающийся ученый и общественный деятель С.Л. Соболев являлся прекрасным педагогом, воспитавшим целую плеяду талантливых учеников и последователей. Он преподавал в Ленинградском государственном университете, Ленинградском электротехническом институте, Военно-транспортной академии РКК, Московском государственном университете, Московском физико-техническом институте, Новосибирском государственном университете.

Блестящая научная и общественная деятельность С.Л. Соболева, определившая его огромный авторитет у нас в стране, получила международное признание. Он являлся иностранным членом Французской академии наук, иностранным членом Национальной академии деи Линчеи в Риме, иностранным членом академии наук в Берлине, почетным членом Эдинбургского Королевского общества, почетным членом Московского и Американского математических обществ, почетным доктором многих университетов мира. Заслуги С.Л. Соболева отмечены многочисленными государственными наградами. Президиум АН СССР присудил С.Л. Соболеву за 1988 год золотую медаль им. М.В. Ломоносова за выдающиеся достижения в области математики. 

Сергей Львович Соболев скончался 3 января 1989 года в г. Москве, похоронен на Новодевичьем кладбище.

 

Материалы о С.Л. Соболеве

Биобиблиографические материалы

Хронологические указатели трудов С.Л. Соболева

Литература о жизни и деятельности С.Л. Соболева

 

Мемориальная доска на здании Института математики им. С.Л. Соболева СО РАН

Стенды, посвященные С.Л. Соболеву (сделаны и размещены в Институте математики им. С.Л. Соболева СО РАН)
 

Фотографии С.Л. Соболева

В начало