Демиденко Г.В. Матричные уравнения. Учебное пособие. Новосибирск: Изд-во Новосиб. ун-та, 2009. 203 с.
|
|
|
В учебном пособии изучаются различные матричные уравнения, возникающие при решении ряда спектральных задач линейной алгебры, при исследовании устойчивости решений систем обыкновенных дифференциальных и разностных уравнений, при изучении некоторых задач механики и т. д. Наряду с классическими матричными уравнениями (уравнения Сильвестра, матричные и дифференциальные уравнения Ляпунова) рассматриваются некоторые уравнения, появившиеся в прикладных задачах относительно недавно. Основными вопросами при изучении матричных уравнений являются теоремы существования и единственности решения, формулы решений, теоремы о возмущении и непрерывной зависимости решений от исходных данных, построение приближенных решений, приложения.
Пособие предназначено для студентов старших курсов, аспирантов и преподавателей механико-математического факультета, факультета информационных технологий и физического факультета Новосибирского государственного университета.
Введение
Глава 1. Матричные уравнения Сильвестра -
Ляпунова - Крейна
§ 1. Примеры матричных уравнений Сильвестра
- Ляпунова - Крейна
§ 2. Разрешимость матричных уравнений Сильвестра
- Ляпунова - Крейна
§ 3. Уравнение Сильвестра
§ 4. Уравнение Ляпунова
§ 5. Непрерывная зависимость решений уравнения
Ляпунова
§ 6. Дискретное уравнение Ляпунова
§ 7. Непрерывная зависимость решений дискретного
уравнения Ляпунова
§ 8. Принадлежность матричного спектра области,
ограниченной эллипсом
§ 9. Принадлежность матричного спектра области,
ограниченной параболой
§ 10. Принадлежность матричного спектра множеству,
ограниченному гиперболой
Глава 2. Уравнения Ляпунова и дихотомия матричного спектра
§ 1. Дискретное уравнение Ляпунова и круговая
дихотомия
§ 2. Дихотомия матричного спектра относительно
окружности
§ 3. Дихотомия матричного спектра относительно мнимой
оси
§ 4. Приближенное построение проекторов на
инвариантные подпространства
§ 5. Метод матричной сигнум-функции
§ 6. Трихотомия матричного спектра относительно мнимой
оси
Глава 3. Эволюционные матричные уравнения
§ 1. Дифференциальные матричные уравнения
§ 2. Дифференциальное уравнение Ляпунова
§ 3. Непрерывная зависимость решений дифференциального
уравнения Ляпунова
§ 4. Разрешимость дифференциального уравнения Ляпунова
в случае экспоненциальной дихотомии
§ 5. Разностное матричное уравнение Ляпунова
§ 6. Непрерывная зависимость решений разностного
матричного уравнения Ляпунова
§ 7. Эволюционное уравнение для интегралов типа
Ляпунова
Литература
Настоящее пособие написано на основе курса лекций "Дополнительные главы линейной алгебры" для магистрантов механико-математического факультета и спецкурсов, читавшихся по кафедре дифференциальных уравнений и в учебно-исследовательской лаборатории высокопроизводительных вычислительных систем НГУ-Интел.
В пособии рассматриваются различные матричные уравнения, возникающие при решении задач линейной алгебры, при исследовании устойчивости решений дифференциальных и разностных уравнений, при изучении некоторых задач механики и т. д. Наряду с классическими матричными уравнениями (уравнения Сильвестра, уравнения Ляпунова) рассматриваются некоторые уравнения, появившиеся в литературе относительно недавно.
Основная цель пособия - изложить основы теории линейных матричных уравнений. В частности, изучаются следующие вопросы: теоремы существования и единственности решений, различные формулы решений, непрерывная зависимость решений от исходных данных, построение приближенных решений, примеры использования решений матричных уравнений в некоторых прикладных задачах.
Пособие состоит из трех глав. В первой главе изучаются матричные уравнения вида
введенные М. Г. Крейном (1948). Класс таких уравнений является частным случаем уравнений Сильвестра (1884) и содержит знаменитое матричное уравнение Ляпунова (1892)
и дискретное уравнение Ляпунова
Отметим, что большое количество матричных уравнений вида (0.1), возникающих при решении спектральных задач линейной алгебры и в теории устойчивости динамических систем, содержится в монографиях [20, 23].
Во второй главе рассматриваются уравнения Ляпунова (0.2) и (0.3) в тех случаях, когда, вообще говоря, не выполнены условия однозначной разрешимости. Большой интерес к рассмотрению таких случаев связан с решением задач о дихотомии матричного спектра относительно мнимой оси ("линейная дихотомия") и относительно окружности ("круговая дихотомия"). Теоретические исследования этих задач проводились в 40-е годы прошлого столетия в работах М. Г. Крейна (см. [11]). В работе А. А. Абрамова [1] был предложен известный метод матричной сигнум-функции, позволяющий численно решать задачи о дихотомии. Исследования С. К. Годунова и А. Я. Булгакова, проводимые в 80-е годы, привели к разработке численных алгоритмов решения задач о дихотомии с гарантированной точностью (см. [9, 10, 31]). В последних трех параграфах приводятся некоторые варианты приближенного построения проекторов, возникающих в задачах о дихотомии. В основу построения таких приближений положен функциональный подход [15].
В третьей главе рассматриваются эволюционные матричные уравнения. В частности, изучаются дифференциальное уравнения Ляпунова
и разностное матричное уравнение Ляпунова
с периодическими коэффициентами. Уравнение (0.4) возникает в теории устойчивости решений систем дифференциальных уравнений с периодическими линейными членами
Уравнение (0.5) возникает в связи с исследованием устойчивости решений систем разностных уравнений с периодическими линейными членами
В главе доказываются теоремы о разрешимости матричных уравнений (0.4) и (0.5), выводятся формулы решений, изучается непрерывная зависимость периодических решений от коэффициентов. Эти результаты используются при изучении асимптотической устойчивости стационарных решений систем (0.6) и (0.7). В частности, критерий асимптотической устойчивости нулевого решения линейной системы дифференциальных уравнений (0.6) формулируется в терминах разрешимости следующей краевой задачи
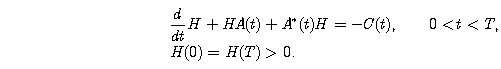
Отметим, что на основе аналогичных
результатов можно получить новое доказательство [17] устойчивости верхнего
положения равновесия маятника при достаточно большой частоте перемещения точки
подвеса. Этот красивый и, на первый взгляд, неожиданный результат хорошо
известен в литературе (см., например, [5, 27]) и вытекает из доказательства
асимптотической устойчивости стационарного решения
дифференциального
уравнения
Это уравнение описывает движение маятника,
когда вертикальное перемещение точки подвеса происходит по закону
,
при этом 
-
угол отклонения маятника от вертикального положения,
-
коэффициент затухания,
-
длина маятника,
-
ускорение свободного падения (
).
В последнем параграфе приводится еще одно эволюционное матричное уравнение
которое также возникает в задачах об устойчивости решений дифференциальных уравнений.
Основная часть содержания главы 3 написана на основе работ [2, 3, 6, 12, 14-18, 25, 26, 32].
Все главы пособия разбиты на параграфы. В конце каждого параграфа содержатся задачи, часть из которых носит исследовательский характер. Некоторые из результатов, сформулированных в задачах, используются в основном тексте пособия.
Для изучения представленного материала читателю потребуются некоторые сведения из университетских курсов по линейной алгебре [7, 30], теории функций комплексного переменного [4], обыкновенным дифференциальным и разностным уравнениям [8, 19], функциональному анализу [22, 29], теории соболевских пространств [13].
Автор выражает глубокую благодарность академику С. К. Годунову за предоставленную возможность чтения курса лекций для магистрантов "Дополнительные главы линейной алгебры" и за дискуссии по спектральным проблемам линейной алгебры, канд. физ.-мат. наук И. И. Матвеевой за неоценимую помощь в работе, д-ру физ.-мат. наук Ю. С. Волкову и канд. физ.-мат. наук В. И. Костину за предложение прочитать спецкурс "Матричные уравнения" в учебно-исследовательской лаборатории высокопроизводительных вычислительных систем НГУ-Интел.
