Laboratory "Mathematical Methods of Decision Making"
Sobolev Institute of
Mathematics
Laboratory "Mathematical Methods
of Decision Making"
| Dr. Yuri Kochetov
|
 Yuri Kochetov Curriculum Vitae Publications Conference presentations
Industrial experience  Benchmarks
library |
Benchmarks library
UNCAPACITATED FACILITY LOCATION PROBLEM
GIVEN:
Finite sets of facilities I = { 1, ..., n } and clients J = { 1, ..., m }, a nonnegative vector ci , i I and a matrix gij , i
FIND:
Nonempty subset S
I which minimize the objective function:
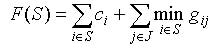
Software for the Local Search Algorithms for Windows-95 (zip-file 227 Kb)
1. INSTANCES WITH LARGE DUALITY GAP
The instances are generated at random with the following parameters:
n = m = 100, ci = 3000, Ij
I, | Ij |=10,
gijIj , j
Three types of matrices gij are considered: classes A, B, C.
Class A
The matrix gij has exactly 10 noninfinity elements for each column j.
The branch and bound algorithm runs approximately 10 million nodes to find an optimal solution.
Benchmarks generator for Windows-95 (zip-file 173 Kb) Results
Class B
The matrix gij has exactly 10 noninfinity elements for each row i.
The branch and bound algorithm runs approximately 30 million nodes to find an optimal solution.
Benchmarks generator for Windows-95 (zip-file 174 Kb) Results
Class C
The matrix gij has exactly 10 noninfinity elements for each row i and each column j. The branch and bound algorithm runs more than 500 million nodes to find an optimal solution.
Benchmarks generator for Windows-95 (zip-file 174 Kb) Results
2. INSTANCES ON FINITE PROJECTIVE PLANES
The instances are based on the incidence matrices for the finite projective planes. If the plane has dimension k we generate UFLP instances for n=k2+k+1 facilities and m=n clients. The fixed costs ci equal 3000. The matrix gij has exactly n+1 noninfinity elements from the set {0,1,2,3,4} for each row i and column j. Optimal solutions have (n+1) opening facilities and can be found in polynomial time.