Методы нахождения оценок: метод максимального правдоподобия

Метод максимального правдоподобия — еще один разумный способ построения оценки неизвестного параметра. Состоит он в том, что в качестве «наиболее правдоподобного» значения параметра берут значение $\theta$ , максимизирующее вероятность получить при

опытах данную выборку ${\mathbf X}=(X_1, \ldots, X_n)$ . Это значение параметра $\theta$ зависит от выборки и является искомой оценкой.

Решим сначала, что такое «вероятность получить данную выборку», т.е. что именно нужно максимизировать. Вспомним, что для абсолютно непрерывных распределений $\mathscr F_\theta$ их плотность $f_\theta(y)$ — «почти» (с точностью до

) вероятность попадания в точку

. А для дискретных распределений $\mathscr F_\theta$ вероятность попасть в точку

равна ${\mathsf P}_\theta\,(X_1=y)$ . И то, и другое мы будем называть плотностью распределения $\mathscr F_\theta$ . Итак,

Для тех, кто знаком с понятием интеграла по мере, нет ничего странного в том, что мы ввели понятие плотности для дискретного распределения. Это — не плотность относительно меры Лебега, но плотность относительно считающей меры.

Если для дискретного распределения величины со значениями , , $\ldots$ ввести считающую меру $\char93$ на борелевской $\sigma$ -алгебре как

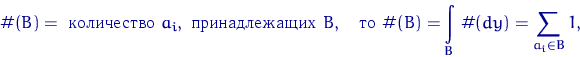
$\begin{displaymath} \char93 (B)=\textrm{ количество } a_i, \textrm{ принадлежащи... ...har93 (B)=\int\limits_B \,\char93 (dy)=\sum\limits_{a_i\in B}1,\end{displaymath}$

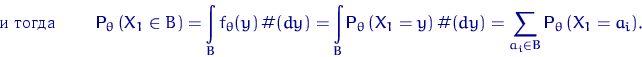
$\begin{displaymath} \textrm{ и тогда \quad \quad } {\mathsf P}_\theta\,(X_1\in B... ...sum\limits_{a_i\in B}{\mathsf P}_\theta\,(X_1=a_i).\quad \quad \end{displaymath}$

Если же

имеет абсолютно непрерывное распределение, то $f_\theta(y)$ есть привычная плотность относительно меры Лебега $\lambda(dy)=dy$ :

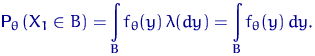
$\displaystyle{\mathsf P}_\theta\,(X_1\in B)=\int\limits_B f_\theta(y)\,\lambda(dy)= \int\limits_B f_\theta(y)\,dy.$

Определение 6.

Функция (случайная величина при фиксированном $\theta$ )

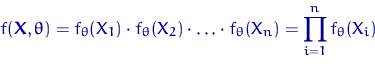
$\begin{displaymath} f({\mathbf X}, \theta) = f_\theta(X_1)\cdot f_\theta(X_2) \c... ...\ldots \cdot f_\theta(X_n) = \prod\limits_{i=1}^n f_\theta(X_i)\end{displaymath}$

называется функцией правдоподобия. Функция (тоже случайная)

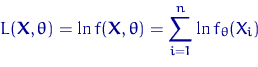
$\begin{displaymath} L({\mathbf X}, \theta) = \ln f({\mathbf X}, \theta) = \sum\limits_{i=1}^n \ln f_\theta(X_i)\end{displaymath}$

называется логарифмической функцией правдоподобия.

В дискретном случае функция правдоподобия $f(x_1,\ldots,x_n,\, \theta)$ есть вероятность выборке

, $\ldots$ ,

в данной серии экспериментов равняться

, $\ldots$ ,

. Эта вероятность меняется в зависимости от $\theta$ :

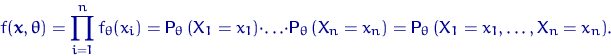
$\begin{displaymath} f({\mathbf x}, \theta) = \prod\limits_{i=1}^n f_\theta(x_i) ... ...ta\,(X_n=x_n) = {\mathsf P}_\theta\,(X_1=x_1, \ldots, X_n=x_n).\end{displaymath}$

Определение 7.

Оценкой максимального правдоподобия $\hat\theta$ неизвестного параметра $\theta$ называют значение $\theta$ , при котором функция $f({\mathbf X}, \theta)$ достигает максимума (как функция от $\theta$ при фиксированных $X_1, \ldots, X_n$ ):

$\begin{displaymath} \hat\theta = \textrm{arg}~ \max_{\theta} f({\mathbf X}, \theta).\end{displaymath}$

Замечание 7.

Поскольку функция $\ln y$ монотонна, то точки максимума $f({\mathbf X}, \theta)$ и $L({\mathbf X}, \theta)$ совпадают. Поэтому оценкой максимального правдоподобия (ОМП) можно называть точку максимума (по $\theta$ ) функции $L({\mathbf x}, \theta)$ :

$\begin{displaymath} \hat\theta = \textrm{arg}~ \max_{\theta} L({\mathbf X}, \theta).\end{displaymath}$

Напомним, что точки экстремума функции — это либо точки, в которых производная обращается в нуль, либо точки разрыва функции/производной, либо крайние точки области определения функции.

Пример 7.

Пусть , $\ldots$ , — выборка объема из распределения Пуассона $\text{\boldmath\ensuremath \Pi}_\lambda$ , где $\lambda\gt$ . Найдем ОМП $\hat\lambda$ неизвестного параметра $\lambda$ .

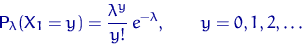
$\begin{displaymath} {\mathsf P}\,{\!}_\lambda(X_1=y)=\dfrac{\lambda^y}{y!}\,e^{-\lambda}, \qquad y=0,1,2,\ldots\end{displaymath}$

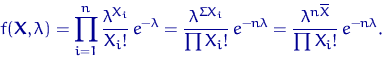
$\begin{displaymath} f({\mathbf X}, \lambda)=\prod\limits_{i=1}^n \dfrac{\lambda^... ...a}= \dfrac{\lambda^{n\overline X}}{\prod X_i!}\, e^{-n\lambda}.\end{displaymath}$

Поскольку эта функция при всех $\lambda\gt$ непрерывно дифференцируема по $\lambda$ , можно искать точки экстремума, приравняв к нулю частную производную по $\lambda$ . Но удобнее это делать для логарифмической функции правдоподобия:

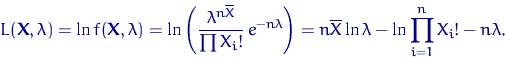
$\begin{displaymath} L({\mathbf X}, \lambda)=\ln f({\mathbf X}, \lambda)= \ln \le... ...rline X \ln \lambda - \ln \prod\limits_{i=1}^n X_i! - n\lambda.\end{displaymath}$

Тогда

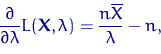
$\begin{displaymath} \dfrac{\partial}{\partial\lambda} L({\mathbf X}, \lambda) =\dfrac{n\overline X}{\lambda} - n,\end{displaymath}$

и точка экстремума $\hat\lambda$ — решение уравнения: $\dfrac{n\overline X}{\lambda} - n = 0$ , то есть $\hat\lambda=\overline X$ .

Пример 8.

Пусть , $\ldots$ , — выборка объема из нормального распределения ${\mathsf N}_{a,\sigma^2}$ , где $a\in {\textrm{\upshape I\kern-0.20em R}}$ , $\sigma\gt$ ; и оба параметра , $\sigma^2$ неизвестны.

Выпишем плотность, функцию правдоподобия и логарифмическую функцию правдоподобия. Плотность:

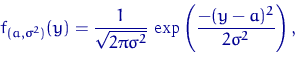
$\begin{displaymath} f_{(a,\sigma^2)}(y)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\, \exp\left(\dfrac{-(y-a)^2}{2\sigma^2}\right),\end{displaymath}$

функция правдоподобия:

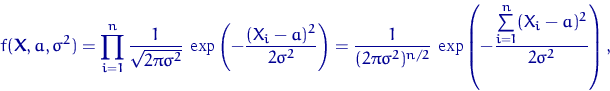
$\begin{displaymath} f({\mathbf X}, a,\sigma^2)=\prod\limits_{i=1}^n \dfrac{1}{\s... ...\left(-\dfrac{\sum\limits_{i=1}^n (X_i-a)^2}{2\sigma^2}\right),\end{displaymath}$

логарифмическая функция правдоподобия:

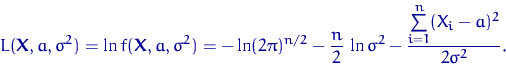
$\begin{displaymath} L({\mathbf X}, a,\sigma^2)=\ln f({\mathbf X}, a,\sigma^2) = ... ...,\ln\sigma^2 -\dfrac{\sum\limits_{i=1}^n (X_i-a)^2}{2\sigma^2}.\end{displaymath}$

В точке экстремума (по $(a,\sigma^2)$ ) гладкой функции обращаются в нуль обе частные производные:

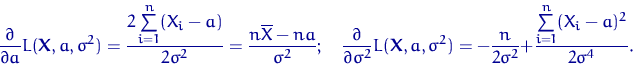
$\begin{displaymath} \dfrac{\partial}{\partial a} L({\mathbf X}, a,\sigma^2) = \d... ...}{2\sigma^2} +\dfrac{\sum\limits_{i=1}^n (X_i-a)^2}{2\sigma^4}.\end{displaymath}$

Оценка максимального правдоподобия $(\hat a, \hat{\sigma^2})$ для $(a,\sigma^2)$ — решение системы уравнений

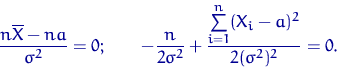
$\begin{displaymath} \dfrac{n \overline X - n a}{\sigma^2}=0; \quad \quad - \dfra... ...ma^2} +\dfrac{\sum\limits_{i=1}^n (X_i- a)^2}{2(\sigma^2)^2}=0.\end{displaymath}$

Решая, получим хорошо знакомые оценки:

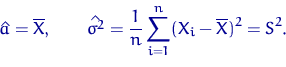
$\begin{displaymath} \hat a=\overline X, \qquad \hat{\sigma^{2}} = \dfrac{1}{n} \sum\limits_{i=1}^n (X_i-\overline X)^2=S^2.\end{displaymath}$

Пример 9.

Пусть , $\ldots$ , — выборка объема из равномерного распределения ${\mathsf U}_{0,\theta}$ , где $\theta\gt$ . Тогда $\hat\theta=X_{(n)}$ (см. [3, пример 4.4, с.24] или [1, пример 5, с.91]).

Пример 10.

Пусть , $\ldots$ , — выборка объема из равномерного распределения ${\mathsf U}_{\theta,\theta+5}$ , где $\theta\in{\textrm{\upshape I\kern-0.20em R}}$ (см. также [1, пример 4, с.91]).

Выпишем плотность распределения и функцию правдоподобия. Плотность:

$\begin{displaymath} f_{\theta}(y)=\begin{cases} 1/5, & \textrm{ если } y\in[\theta,\theta+5] \cr 0 & \textrm{ иначе}, \end{cases}\end{displaymath}$

функция правдоподобия:

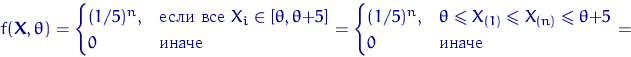
$\begin{displaymath} f({\mathbf X},\theta)=\begin{cases} (1/5)^n, & \textrm{если ... ..._{(n)}\leqslant\theta{+}5 \cr 0 & \textrm{иначе }\end{cases}= \end{displaymath}$

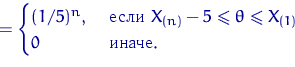
$\begin{displaymath} =\begin{cases} (1/5)^n, & \textrm{ если } X_{(n)}-5\leqslant\theta\leqslant X_{(1)} \cr 0 & \textrm{ иначе}. \end{cases}\end{displaymath}$

Функция правдоподобия достигает своего максимального значения во всех точках $\theta\in[X_{(n)}-5, X_{(1)}]$ . График этой функции изображен на рис. 4.

Рис. 4: Пример 10.

$\begin{figure} \unitlength=0.8mm \begin{picture} (60.00,25.00)(0,-10) \put(5.00,... ...0.00,35.00){\makebox(0,0)[lc]{$f({\mathbf X},\theta)$}}\end{picture}\end{figure}$

**Рис. 4:** Пример 10.
$\begin{figure} \unitlength=0.8mm \begin{picture} (60.00,25.00)(0,-10) \put(5.00,... ...0.00,35.00){\makebox(0,0)[lc]{$f({\mathbf X},\theta)$}}\end{picture}\end{figure}$

Любая точка может служить оценкой максимального правдоподобия. Получаем более чем счетное число оценок вида

$\begin{displaymath} \hat\theta_\alpha=(1-\alpha)(X_{(n)}-5)+\alpha X_{(1)}\end{displaymath}$

при разных $\alpha\in [0,\,1]$ , в том числе и , — концы отрезка.

Упражнение.

1) Убедиться, что отрезок $[X_{(n)}-5, X_{(1)}]$ не пуст.

2) Найти оценку метода моментов (по первому моменту) и убедиться, что она иная по сравнению с ОМП. 3) Найти ОМП параметра $\theta$ равномерного распределения ${\mathsf U}_{\theta,2\theta}$ .

2.5. Методы нахождения оценок: метод максимального правдоподобия