next up previous index
Next:  Критерий Фишера   Up:  Критерии согласия   Previous:  Проверка гипотезы однородности

8.5.   Проверка гипотезы независимости: критерий хи-квадрат Пирсона

Есть выборка $({\mathbf X},{\mathbf Y})=\bigl((X_1,Y_1),\ldots,(X_n,Y_n)\bigr)$ значений двух наблюдаемых совместно случайных величин $X$ и $Y$ в $n$ независимых экспериментах. Проверяется гипотеза $H_1=\{X \textrm{ и } Y \textrm{ независимы}\}$.

Введем $k$ интервалов группировки $\Delta_1, \ldots, \Delta_k$ для значений $X$ и $m$ интервалов группировки $\nabla_1, \ldots, \nabla_m$ для значений $Y$.

Посчитаем эмпирические частоты:

$ \nu_{i,j}=\{\textrm{число~пар~} (X_l,Y_l), \textrm{~попавших~в~} \Delta_i{\times}\nabla_j\}, $

$ \nu_{\cdot,j}=\{\textrm{число~} Y_l, \textrm{ попавших в }\nabla_j\}, $ $ \nu_{i,\cdot}=\{\textrm{число~} X_l, \textrm{ попавших в }\Delta_i\}. \ $

${\mathbf Y}$

${\mathbf X}$

$\nabla_1$
 		 $\nabla_2$
 		 $\ldots$
 		 $\nabla_m$
 		 $\sum\limits_{j=1}^m$
 
$\Delta_1$$\nu_{11}$$\nu_{12}$$\ldots$$\nu_{1m}$$\nu_{1\cdot}$
$\vdots$     $\ldots$  $\vdots$
$\Delta_k$$\nu_{k1}$$\nu_{k2}$$\ldots$$\nu_{km}$$\nu_{k\cdot}$
$\sum_{i=1}^k$$\nu_{\cdot 1}$$\nu_{\cdot 2}$$\ldots$$\nu_{\cdot m}$$n$


Если гипотеза $H_1$ верна, то теоретические вероятности попадания пары $(X,Y)$ в любую из областей $\Delta_i\times\nabla_j$ равны произведению вероятностей: для всех $i$ и $j$

\begin{displaymath} p_{i,j}={\mathsf P}\,\bigl((X,Y)\in\Delta_i\times\nabla_j\bi... ...igr)\cdot{\mathsf P}\,\bigl(Y\in\nabla_j\bigr)=p_i^x\cdot p_j^y\end{displaymath}.

Именно эту гипотезу (назовем ее $H_1'$) мы в действительности и проверяем.

По ЗБЧ

\begin{displaymath} \dfrac{\nu_{i,\cdot}}{n} \buildrel {p} \over \longrightarrow... ...frac{\nu_{i,j}}{n} \buildrel {p} \over \longrightarrow p_{i,j}.\end{displaymath}

Поэтому значительная разница между $\dfrac{\nu_{i,j}}{n}$ и $\dfrac{\nu_{i,\cdot}}{n}\,\dfrac{\nu_{\cdot,j}}{n}$ (или между $\nu_{i,j}$ и $\dfrac{\nu_{i,\cdot}\,\nu_{\cdot,j}}{n}$) может служить основанием для отклонения гипотезы независимости.

Пусть

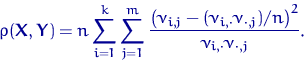\begin{equation} \rho({\mathbf X},{\mathbf Y})=n\sum_{i=1}^k\sum_{j=1}^m \dfrac{... ...u_{i,\cdot}\nu_{\cdot,j})/n\bigr)^2} {\nu_{i,\cdot}\nu_{\cdot,j}}.\end{equation}(26)

Теорема 10.

Если гипотеза $H_1$ верна, то $\rho({\mathbf X},{\mathbf Y})\Rightarrow {\mathsf H}_{(k-1)(m-1)}$ при $n\to\infty$.

Критерий согласия асимптотического уровня $\varepsilon$ строится обычным образом.

Упражнение.    Чтобы функция $\rho$ и теорема 10 не падали с неба, убедитесь, что гипотеза $H_1'$ есть гипотеза о принадлежности распределения выборки параметрическому семейству распределений с вектором неизвестных параметров $(p_1^x,\ldots,p_{k-1}^x, p_1^y,\ldots,p_{m-1}^y)$ размерности $l{=}k{+}m{-}2$.

Подставив оценки максмального правдоподобия ${\nu_{i,\cdot}}/{n}$ для $p_i^x$   и   ${\nu_{\cdot,j}}/{n}$ для $p_j^y$ в функцию

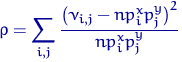\begin{displaymath} % latex2html id marker 9857 \rho=\sum_{i,j}\dfrac{\bigl(\nu_... ...j^y\bigr)^2}{np_i^xp_j^y} \end{displaymath}   (см. (24))

получим (26). Всего есть $k\cdot m$ интервалов, и по теореме 8 при верной $H_1'$ предельное $\chi^2$-распределение имеет $k{\cdot}m{-}1{-}(k{+}m{-}2)=(k{-}1)(m{-}1)$ степеней свободы.


Замечания 19 и 20 по поводу числа $k\cdot m$ интервалов группировки остаются в силе.


N.I.Chernova
9 сентября 2002