Есть две независимые
выборки: ![]() из
из ![]() и
и
![]() из
из ![]() , причем дисперсия
, причем дисперсия ![]() одинакова для обоих распределений,
но, вообще говоря, неизвестна.
Проверяется сложная гипотеза
одинакова для обоих распределений,
но, вообще говоря, неизвестна.
Проверяется сложная гипотеза ![]() .
.
Эта задача есть частный случай задачи об однородности.
Для ее решения построим критерий Стьюдента точного размера ![]() .
.
Из леммы Фишера вытекает следующее утверждение.
Доказательство теоремы 12.
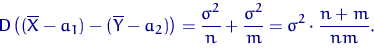
Нормируем эту разность. Величина
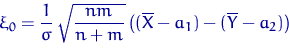
имеет стандартное нормальное распределение.
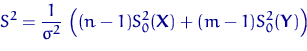
имеет ![]() -распределение
-распределение ![]() с
с ![]() степенями свободы
и не зависит от
степенями свободы
и не зависит от ![]() и от
и от ![]() .
.
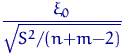 как раз имеет распределение
Стьюдента
как раз имеет распределение
Стьюдента Q.D.E.
Введем функцию
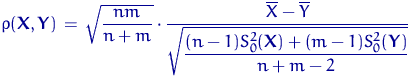 .
.
Из теоремы 12
следует свойство K1(a):
если ![]() верна, т.е. если
верна, т.е. если ![]() , то величина
, то величина
![]() имеет распределение
Стьюдента
имеет распределение
Стьюдента ![]() .
.
Указание. Воспользовавшись ЗБЧ или свойствами 2-4 из 1-й лекции, доказать, что числитель и знаменатель сходятся к постоянным:
![]()
тогда как корень перед дробью неограниченно возрастает.
Поэтому остается по ![]() найти
найти
![]() — квантиль распределения
— квантиль распределения ![]() . Для
такого
. Для
такого ![]() величина
величина ![]() из распределения
из распределения ![]() удовлетворяет
равенству
удовлетворяет
равенству
![]()
И критерий Стьюдента выглядит как все критерии согласия:

N.I.Chernova