Greedy Lattice Animals

Martin, James (Paris, France)
James.Martin@ens.fr

I will survey various aspects of the greedy lattice animals model.

Let $d\geq2$, and let $\{X_\mathbf{v}, \mathbf{v}\in \mathbb {Z} ^d\}$ be an i.i.d. family of non-negative random variables, with common distribution $F$. For a finite subset $\xi$ of $\mathbb {Z} ^d$, the weight $S(\xi)$ of $\xi$ is defined by

$$S(\xi)=\sum_{\mathbf{v}\in\xi} X_\mathbf{v}.$$

A greedy lattice animal of size $n$ is a connected subset of $\mathbb {Z} ^d$ of size $n$ containing the origin, whose weight is maximal among all such sets. Let $N(n)$ be this maximum weight.

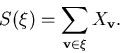
This model has a variety of applications in percolation, statistical physics and queueing theory. It was introduced by Cox, Gandolfi, Griffin and Kesten, who showed that if

$${\mathsf E}\,X_{{{\boldsymbol{0}}}}^d(\log^+ X_{{{\boldsymbol{0}}}})^{d+\epsilon} < \infty \text{ for some } \epsilon\gt,$$

then there exists an $N<\infty$ such that

 $$\frac{N(n)}{n}\to N \text{ almost surely and in }\mathcal{L}_1.$$

I will present a rather simpler argument to give (1) under the slightly weaker condition that

$$\int_0^\infty\big(1-F(x)\big)^{1/d}dx<\infty,$$

and to give the bound

$$N\leq c\int_0^\infty \big(1-F(x)\big)^{1/d}dx$$

for some constant $c=c(d)$ independent of $F$.

Further topics include: large deviations for $N(n)$; extensions to cases where $X_\mathbf{v}$ may be negative; continuity of $N$ as a function of $F$.

I will mention related models including greedy lattice paths and directed last-passage percolation, and also various associated open problems.