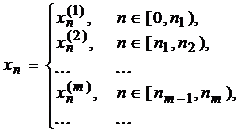
Система QPSLab для анализа и распознавания числовых последовательностей с квазипериодической структурой
Основные понятия и определения
Числовую последовательность xn, n = 0,1,..., с изменяющейся формулой общего члена или последовательность с изменяющимися свойствами можно представить в виде
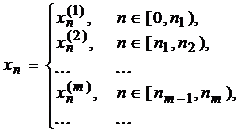
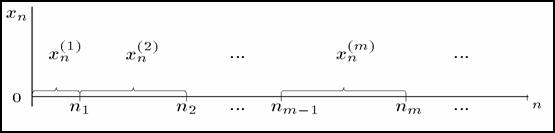
Если положить n0 = 0, то в этой формуле [nm-1, nm), m = 1,2,..., – интервал постоянства свойств последовательности, а nm, m = 1,2,..., – номер члена последовательности, соответствующий смене ее свойств (см. рисунок).
Последовательность, у которой
nm – nm–1 = T, m = 1,2,...,
где T – натуральная константа, называется последовательностью с периодическим изменением свойств.
Последовательность, у которой
nm – nm–1 = T + δ, m = 1,2,...,
где T – натуральная константа, а δ – случайная величина, математическое ожидание которой равно нулю, называется последовательностью с почти периодическим изменением свойств.
Последовательность, у которой
Tmin ≤ nm – nm–1 ≤ Tmax, m = 1,2,...,
где Tmin и Tmax – натуральные константы, называется последовательностью с квазипериодическим изменением свойств.
Под числовой последовательностью с квазипериодической структурой подразумевается всякая числовая последовательность, включающая такие фрагменты (подпоследовательности подряд расположенных членов), которые имеют характерные детерминированные или стохастические свойства, причем для всех пар следующих друг за другом фрагментов разность между номерами первых членов последующего и предыдущего фрагментов лежит в фиксированном интервале. Последовательность, имеющая квазипериодическую структуру, или квазипериодическая последовательность ― это последовательность с квазипериодической сменой своих свойств. Под сменой свойств детерминированной последовательности понимается, в частности, изменение формулы общего члена, а для стохастической ― изменение ее каких-либо вероятностных характеристик.
Важной разновидностью последовательностей, имеющих квазипериодическую структуру, являются последовательности, которые включают квазипериодически перемежающиеся ненулевые информационные фрагменты одинаковой размерности. Пример такой последовательности приведен на следующем рисунке.
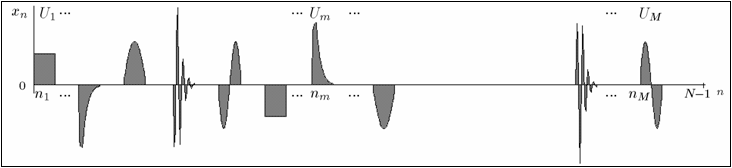
Числовая последовательность, включающая квазипериодически перемежающиеся ненулевые информационные фрагменты размерности q, определяется следующей формулой общего члена:
![]()
где
un-nm (m) = 0, если n-nm ≠ 0,...,q - 1,
0 < ||(u0(m),..., uq-1(m))|| < ∞ при каждом m Î M ={1,...,M},
(n1,…, nM) Î Ω,
причем
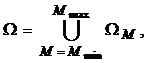
|
ΩM = {(n1,…, nM) | |
0 ≤ n1 ≤ N + ≤ N – q, 0 ≤ N – ≤ nM ≤ N – q, |
| 0 < q ≤ Tmin ≤ nm – nm–1 ≤ Tmax ≤ N – q, m = 2,…, M }, | |
|
|
M Î [Mmin, Mmax], |
а Mmin и Mmax находятся из входящей в определение множества ΩM системы ограничений, в которой N –, N +, Tmin, Tmax – целые числа.
Набор Um = (u0(m),...,uq-1(m)), m Î M, называется информационным вектором. Набор (xnm,...,xnm+q-1), m Î M, совпадающий с информационным вектором, называется информационным фрагментом.
Справедливы следующие оценки для мощности множеств:
| ΩM | = O[(N – q + 1)(Tmax – Tmin + 1)M–1],
| Ω | = O[(N – q + 1)(Mmax – Mmin + 1)(Tmax – Tmin + 1)Mmax–1],
причем M и Mmax – кусочно-постоянные возрастающие функции от N.
Вектор X = (x0,...,xN-1), последовательность компонент которого включает перемежающиеся информационные фрагменты, есть функция X(n1,...,nM, U1,...,UM) от двух наборов (n1,...,nM) и (U1,..., UM). Далее, по мере усложнения формулировок типовых задач эта функция уточняется.
|
предыдущая |
следующая |