Система QPSLab для анализа и распознавания числовых последовательностей с квазипериодической структурой
Проблема обнаружения фрагментов и разбиения последовательности на серии идентичных фрагментов
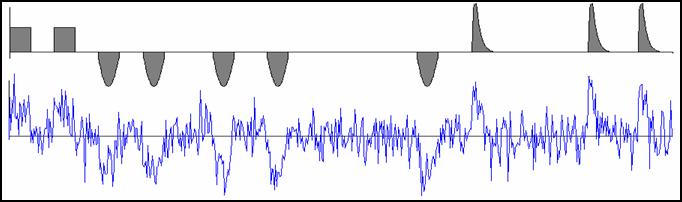
Числовая квазипериодическая последовательность, определяющаяся следующей формулой общего члена (модель без вставок):
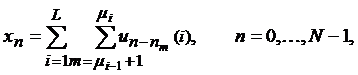
(U1,...,UL) – набор векторов, порождающих серии идентичных фрагментов;
0 = μ0 < μ1 < ... < μL, L ≤ μL – ограничения, определяющие допустимые границы серий;
ΔL(M) = {(μ1,..., μL): 0 < μ1 < ... < μL, L ≤ μL ≤ M};
Y = X(n1,...,nμL, μ1,..., μL, U1,...,UL) + E;
μL = M, |ΔL(M)| = CL-1M-1 – число способов разбиения M участков на L серий.
Имеем следующие возможные задачи
|
Задан эталонный набор |
задан алфавит эталонных фрагментов |
множество фрагментов не ограничено |
|||||||||||||
|
число серий L |
изв. | изв. | неизв. | изв. | неизв. | изв.+изв.число фрагментов в сериях | |||||||||
|
наличие вставок |
нет |
да |
нет |
да |
нет |
да |
нет |
да |
нет |
да |
нет |
да |
|||
| по-теря дан-ных |
нет | число фраг- ментов M
|
изв. | + |
? |
± |
? |
± |
? |
NP-h ? |
? |
NP-h ? |
? |
NP-h
|
NP-h ? |
| неизв. | + | ? | ± | ? | ± | ? |
NP-h ? |
? |
NP-h ? |
? |
|
||||
| есть | изв. | ± | ? | ± | ? | ± | ? |
NP-h ? |
? |
NP-h ? |
? |
NP-h
|
NP-h ? |
||
| неизв. | ± | ? | ± | ? | ± | ? |
NP-h ? |
? |
NP-h ? |
? |
|
||||
|
Здесь используются следующие обозначения: |
|
|
+ |
– обоснован точный полиномиальный алгоритм; |
|
± |
– обоснован, но еще не опубликован точный полиномиальный алгоритм; |
|
? |
– статус сложности не выяснен, какие либо алгоритмы неизвестны; |
|
NP-h |
– задача NP–трудна, какие либо алгоритмы неизвестны; |
|
NP-h? |
– задача скорее всего NP–трудна, какие либо алгоритмы неизвестны. |
|
предыдущая |
следующая |