Система QPSLab для анализа и распознавания числовых последовательностей с квазипериодической структурой
Проблема обнаружения и идентификации фрагментов
Структура последовательности:
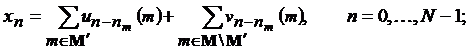
M' Í M = {1,...,M}, |M'| = M';
Y = X + E;
Um Î A, m Î M, – соответствует искомому информационному фрагменту,
Vm Î B, m Î M\M', – фрагменту-вставке (вектору-вставке),
A – множество информационных фрагментов,
B – множество допустимых вставок.
| Задан алфавит информ. фрагментов A | Множество информ. фрагментов не задано | ||||||||||||
|
вставок нет M=M' |
имеются вставки M' Ì M |
вставок нет M=M' |
имеются вставки M' Ì M |
||||||||||
|
задан алфавит вставок B |
множество вставок не ограничено |
|
задан алфавит вставок B |
множество вставок не ограничено |
|||||||||
|
число вставок M – M' |
=0 |
изв.
|
неизв.
|
изв.
|
неизв.
|
=0 |
изв.
|
неизв.
|
изв.
|
неизв.
|
|||
| по-теря дан-ных |
нет | число фраг- ментов M
|
изв. |
+ |
? |
? |
? |
? |
+ |
? |
? |
+ |
+ |
| неизв. | + | ? | ? | ? | ? |
± |
? |
? |
± |
± |
|||
| есть | изв. | + | ? | ? | ? | ? | ± |
? |
? |
± |
± |
||
| неизв. | + | ? | ? | ? | ? | ± |
? |
? |
± |
± |
|||
|
Здесь используются следующие обозначения: |
|
|
+ |
– обоснован точный полиномиальный алгоритм; |
|
± |
– обоснован, но еще не опубликован точный полиномиальный алгоритм; |
|
? |
– статус сложности не выяснен, какие либо алгоритмы неизвестны. |
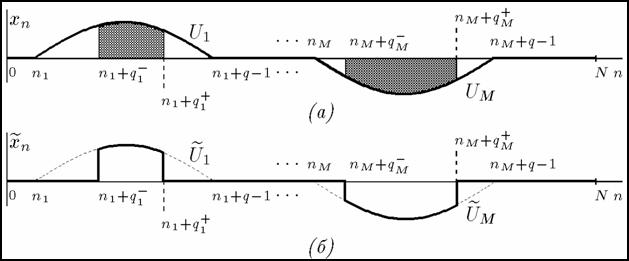
В варианте наличия потери данных рассматривается частный случай потерь, когда начальная и конечная части фрагмента оказываются обнулены, то есть исходная последовательность сформирована из обрывков эталонных фрагментов.
|
предыдущая |
следующая |