Гамма-распределение и его свойства

Next: Распределение «хи-квадрат» Up: Распределения, связанные с нормальным Previous: Распределения, связанные с нормальным

6.1. Гамма-распределение и его свойства

С определением гамма-распределения мы познакомились в курсе теории вероятностей. вспомнить! Нам понадобится свойство устойчивости по суммированию этого распределения, которое до сих пор было доказано только в частном случае — когда независимые слагаемые имеют одно и то же показательное распределение ${\mathsf E}\,{\!}_{\alpha}=\text{\boldmath\ensuremath \Gamma}_{\alpha,1}$ .

Свойство 7.

Пусть $\xi_1$ , $\ldots$ , $\xi_n$ независимы, и $\xi_i$ имеет гамма-распределение $\text{\boldmath\ensuremath \Gamma}_{\alpha,\lambda_i}$ , $i=1, \ldots, n$ . Тогда

$\begin{displaymath} S_n=\sum_{i=1}^n \xi_i \textrm{имеет распределение } \text{\boldmath\ensuremath \Gamma}_{\alpha,\sum_1^n\lambda_i}.\end{displaymath}$ имеет распределение $\text{\boldmath\ensuremath \Gamma}_{\alpha,\sum_1^n\lambda_i}$

Доказательство свойства устойчивости по суммированию (свойства 7.) Воспользуемся свойствами характеристических функций. Характеристическая функция гамма-распределения $\text{\boldmath\ensuremath \Gamma}_{\alpha,\lambda}$ вычислена нами в курсе теории вероятностей и равна

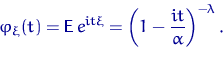
$\begin{displaymath} \varphi_\xi(t)={\mathsf E}\, e^{it\xi}=\left(1-\dfrac{it}{\alpha}\right)^{-\lambda}.\end{displaymath}$

Характеристическая функция суммы независимых случайных величин есть произведение характеристических функций слагаемых:

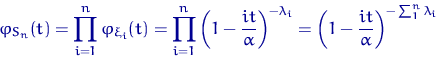
$\begin{displaymath} \varphi_{S_n}(t)=\prod_{i=1}^n \varphi_{\xi_i}(t) = \prod_{i... ...mbda_i}= \left(1-\frac{it}{\alpha}\right)^{-\sum_1^n\lambda_i} \end{displaymath}$

— х.ф. распределения $\text{\boldmath\ensuremath \Gamma}_{\alpha,\sum_1^n\lambda_i}$ .

Q.D.E.

Свойство 8.

Если $\xi$ имеет стандартное нормальное распределение, то $\xi^2$ имеет гамма-распределение $\text{\boldmath\ensuremath \Gamma}_{1/2,1/2}$ .

Доказательство.

Найдем производную функции распределения величины $\xi^2$ и убедимся, что она является плотностью распределения.

При $y\leqslant 0$

$\begin{displaymath} F_{\xi^2}(y)={\mathsf P}\,(\xi^2<y)=0, \textrm{поэтому и плотность } f_{\xi^2}(y)=0.\end{displaymath}$

При $y\gt$

$\begin{displaymath} F_{\xi^2}(y)={\mathsf P}\,(\xi^2<y)={\mathsf P}\,(-\sqrt{y}<\xi<\sqrt{y})=F_\xi(\sqrt{y})- F_\xi(-\sqrt{y}).\end{displaymath}$

Тогда

$\begin{displaymath} f_{\xi^2}(y)=\left(F_{\xi^2}(y)\right)'=F'_\xi(\sqrt{y})\cdot (\sqrt{y})'- F'_\xi(-\sqrt{y})\cdot (-\sqrt{y})'=\end{displaymath}$

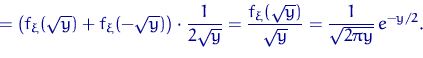
$\begin{displaymath} =\bigl(f_\xi(\sqrt{y})+f_\xi(-\sqrt{y})\bigr)\cdot \dfrac{1... ...f_\xi(\sqrt{y})}{\sqrt{y}}= \dfrac{1}{\sqrt{2\pi y}}\,e^{-y/2}.\end{displaymath}$

Но функция $f_{\xi^2}(y)$ , равная 0 при $y\leqslant 0$ , и равная

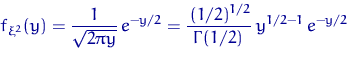
$\begin{displaymath} f_{\xi^2}(y)=\dfrac{1}{\sqrt{2\pi y}}\,e^{-y/2}= \frac{\,(1/2)^{1/2}}{\Gamma(1/2)\,}\, y^{1/2-1}\, e^{-y/2}\end{displaymath}$

при $y\gt$ , является плотностью гамма-распределения $\text{\boldmath\ensuremath \Gamma}_{1/2,1/2}$ .

Q.D.E.

N.I.Chernova 9 сентября 2002