Group Theory Conference in Honor of V.D.Mazurov

Warning: MathJax requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

The \(n^{th}\)-roots of elements of a finite group and their associated digraph

K. Ahmadidelir

Abstract. In this talk, first we introduce a digraph assigned to the \(n^{th}\)-roots of elements of a finite group \(G\) and investigate algebraic properties of this group using the graph theoretical concepts. Then we try to ask and answer some questions about the recognisability and characterising a finite group by its all associated \(n^{th}\)-roots digraphs.

1. Introduction

An element \(g\) of a finite group \(G\) is said to have an \(n^{th}\)-root if there exists an element \(h\in G\) such that \(g=h^n\) (\(n\) is a positive integer). Note that \(g\) may have at least an \(n^{th}\)-root, or it may have none.

Let \(G^n\) be the set of all elements of \(G\) which have at least one \(n^{th}\)-root, i.e.: \[G^n=\{g\in G\mid \exists\; h\in G \;s.t.\; g=h^n\}\]

or, simply, \(G^n=\{g^n\mid g\in G\}\). Then \(P_n(G)=\frac{|G^n|}{|G|}\) is the probability that a randomly chosen element in \(G\) has an \(n^{th}\)-root.

The properties of \(P_2(S_n)\), where \(S_n\) denotes the symmetric group on \(n\) letters have been studied by some authors in [2,5]. Recently, the basic properties of \(P_2(G)\) for an arbitrary finite group \(G\) have been studied (for example, see [3,4]). Already, some years ago in [1], we generalized the probability to \(p^{th}\)-root (\(p > 2\) is a prime number) and gave some bounds for it. We showed that the set \(X=\{P_p(G)\mid G\) is a finite group\(\}\) is a dense subset of the closed interval \([0,1]\).

Now, in some way, we want to use \(n^{th}\)-roots to characterise finite groups. First of all, we introduce a new digraph assigned to the \(n^{th}\)-roots of the elements of a finite group \(G\), as follows:

Definition 1. The digraph associated to the \(n^{th}\)-roots of the elements of a finite group \(G\) is a directed graph whose vertices are whole elements of \(G\) so that any two distinct vertices \(x\) and \(y\) are joined by an edge directed from \(x\) to \(y\) if and only if \(x^n=y\). We denote this digraph by \(\Gamma_n(G)\), or simply by \(\Gamma_n\).

Remark 1. Let \(G\) be a finite group. Some of elementary properties of the digraph \(\Gamma_n(G)\) defined above are:

\(\Gamma_n(G)\) is always planar;

The number of vertices of \(\Gamma_n(G)=|G|\);

In case \(\Gamma_n(G)\) is weakly connected, the number of edges of \(\Gamma_n(G)=|G|-1\); otherwise, \(0\leq \Gamma_n(G)\leq |G|-1\);

The connected component of \(\Gamma_n(G)\) which \(1\) is one of its vertices is in-tree has \(1\) as its sink;

An element of \(G\) is \(n^{th}\)-root of itself if and only if it is a sink in one of the connected component of \(\Gamma_n(G)\) (considering the trivial ones);

An element in \(G\) does not possesses any \(n^{th}\)-root if and only if it is a leaf, so \(|G^n|=V(\Gamma_n(G))\) - the number of leaves (the digraph of \(G^n\) is a subgraph of \(\Gamma_n(G)\) dropping the leaves);

The digraph of \(n^{th}\)-roots of any subgroup of \(G\) is an induced subgraph of \(\Gamma_n(G)\);

\(\Gamma_n(G)\) consists of the digraph of \(n^{th}\)-roots of all cyclic subgroups of \(G\);

Conjugate elements in \(\Gamma_n(G)\) have completely similar positions and inverse elements have symmetric positions;

\(\Gamma_n(G)\) has a dipath of length \(k\) from the vertex \(x\) to the vertex \(y\) if and only if for some \(x^{n^k}=y\) but \(x^{n^{k-1}}\neq y\); particularly, \(\Gamma_n(G)\) has a dipath of length \(k\) from \(g\in G\) to \(1\) if and only if for some \(|g|\,\big|\, n^k\), but \(|g|\nmid n^{k-1}\);

An element \(x\) of \(G\) is \(n^{th}\)-root of itself if and only if \(|x|\,\big|\, n-1\);

Any two distinct elements \(x\) and \(y\) in \(G\) are \(n^{th}\)-root of each other if and only if \(|x|,|y| \,\big|\, n^2-1\) (so, \(|x|,|y|\nmid n-1\));

\(\Gamma_n(G)\) has a cycle of length \(k\) if and only if for some \(g\in G\), \(g^{n^k}=g\) (\(|g|\,\big|\, n^k-1\) but \(|g|\nmid n^{k-1}-1\));

If there is a prime factor \(p\) of \(|x|\) such that \(p\nmid n\), then there is no dipath from \(x\) to \(1\) in \(\Gamma_n(G)\);

If all of prime factors of \(n\) divide \(|x|\), then there is a dipath from \(x\) to \(1\) in \(\Gamma_n(G)\) if and only if \(|x|\,\big|\,n^k\) but \(|x|\nmid n^{k-1}\); on the other hand, if there is a prime factor \(p\) of \(n\) which does not divide \(|x|\), then there is a cycle of length \(k\) from \(x\) to itself or from \(x^i\) to \(x^i\) (for some positive integer \(i\)) if and only if for some positive integer \(j>i\), \(|x|\,\big|\, n^i(n^t-1)\) but \(|x|\nmid n^i(n^s-1)\) for all \(s < t\);

The number of trivial components in \(\Gamma_n(G)\) is equal to \(t-1\), where \(t\) is equal to the number of solutions of the equation \(x^{n-1}=1\) in \(G\) (\(t\) is equal to the number of all of the elements in \(G\) that are \(n^{th}\)-roots of themselves);

The number of elements of \(G\) that arise in a cycle of length \(k\) in \(\Gamma_n(G)\) is equal to the number of solutions of the equation \(x^{n^k-1}=1\) in \(G\), where \(k\) is the least positive integer with this property.

2. Some properties of \(n^{th}\)-roots in finite groups

In this section, we give some elementary results about \(G^n\), where \(G\) is a finite group.

Proposition 2.1 Let \(G\) be a finite group with order \(m\). Let \(n\) be a positive integer. Then \(G^n=G^r\), where \(r\) is the remainder of division of \(n\) by \(m\) (\(n=mq+r;\;\;0\leqslant r < m\)).

Remark 2. By the above proposition, in computing the \(n^{th}\)-roots of a finite group \(G\) of order \(m\) (respectively, computing \(P_n(G)\)), it suffices to compute the \(r^{th}\)-roots only for \(0\leqslant r< m\).

The next propositions reduces the computations of \(G^n\) to \(G^r\), where \(0\leq r<\exp(G)\), the exponent of \(G\).

Proposition 2.2 Let \(G\) be a finite group with exponent \(\exp(G)=e\). Let \(n\) be a positive integer. Then \(G^n=G^r\), where \(r\) is the remainder of division of \(n\) by \(e\) (\(n=eq+r;\;\;0\leq r < e\)).

Proposition 2.3 Let \(G\) be a finite group with exponent \(\exp(G)=e\). Let \(n\) be a positive integer. Then \(G^k=G^{e-k}\) for every integer \(k\), where \(1\leq k\leq e\).

Remark 3. By the above propositions, in computing the \(n^{th}\)-roots of a finite group \(G\) of order \(m\) and exponent \(e\) (and so, computing \(P_n(G)\) and drawing \(\Gamma_n(G)\)), it suffices to compute the \(n^{th}\)-roots only for \(0\leq r< \lfloor \frac{e+1}{2}\rfloor\) (instead of \(0\leq r< e\)). So, \[\forall k=1,\ldots,e-1, \quad P_k(G)=P_{e-k}(G)\] and \(P_e(G)=\frac{1}{|G|}\). On the other hand, for every \(x,y\in G\), \(x^k=y\) if and only if \(x^{e-k}=y^{-1}\), namely, \(x\) is a \(k^{th}\)-root of \(y\) iff \(x\) is a \((e-k)^{th}\)-root of \(y^{-1}\). Therefore, in spite of \(P_k(G)=P_{e-k}(G)\), but the digraphs of \(k^{th}\)-roots and \((e-k)^{th}\)-roots of \(G\) are not the same. Indeed, if the graph of \(k^{th}\)-roots be connected, then to get the digraph of \((e-k)^{th}\)-roots from that, it is sufficient to replace the roots with their inverses from bottom to top of that graph.

3. Some results about the digraph associated to \(n^{th}\)-roots

Let \(p\in \pi(G)\) denote the set of all prime divisors of a finite group \(G\). Then we have:

Theorem 3.1 For a finite group \(G\), \(\Gamma_n(G)\) is in-tree (a digraph that its underlying graph is a tree and have a unique sink), and have \(1\) as its sink, if and only if for all \(p\in \pi(G)\), \(p|n\).

Corollary 3.2 Let \(G\) be a finite group of order \(m\) and \(e=exp(G)\). Then \(\Gamma_n(G)\) is as follows: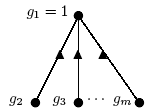

In particular, an abelian group \(G\) is an elementary abelian \(p\)-group of order \(m\) if and only if \(\Gamma_p(G)\) is as above.

4. Recognition of a finite group by its associated digraphs \(\Gamma_n\)

In recent years, there have appeared many "recognition problems", such as:

recognition of a finite group by its commuting graph,
recognition of a finite group by its non-commuting graph,
recognition of a finite group by its prime graph,
recognition of a finite group by its spectrum (the set of element orders of \(G\)).

There are many published papers about the characterization of finite groups (especially, simple ones) by these recognition problems. So, we have a good motivation to introduce another one. In this section, we want to discuss the recognition of a finite group by its associated digraphs of \(n^{th}\)-roots of elements. Now, the question is:

Can we characterize the finite group \(G\) with some of \(\Gamma_n(G)\), where \(1\leq n\leq exp(G)\), up to isomorphism? In other words, are these diagrams another recognition test for a finite group \(G\)?

By the results of previous sections, we have the following theorem:

Theorem 4.1 Two finite abelian groups \(G\) and \(H\) with same exponent \(e\) are isomorphic if and only if, for all \(n\), \(1\leq n\leq e\), \(\Gamma_n(G)\cong\Gamma_n(H)\).

But some of the \(\Gamma_n\)'s (for some \(n\)'s) are redundant. For example, \(\Gamma_1\) and \(\Gamma_e\) (\(e\) is the exponent of these groups) are trivial ones (they are the same in all of the groups with the same exponent). So, the next question is:

What is the least number of these diagrams to recognize a given group with them and which ones are necessary (irredundant)?

For example, we can recognize the quaternion group \(Q_8\) by a \(\Gamma_n\) diagram (for some \(n\)) as follows (it is the unique group up to isomorphism with this diagram):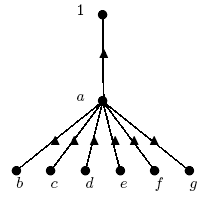

But we can recognize the dihedral group \(D_8\) by a diagram \(\Gamma_n\) (for some \(n\)) as follows: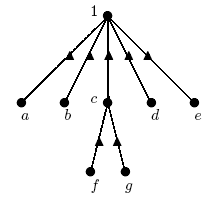

On the other hand:

\(\{P_n(Q_8)\mid 1\leq n \leq e\}=\{1,\frac{1}{4},1,\frac{1}{8}\},\)
\(\{P_n(D_8)\mid 1\leq n \leq e\}=\{1,\frac{1}{4},1,\frac{1}{8}\}.\)

So, the above diagrams can characterise \(Q_8\) and \(D_8\), but their probability of having \(n^{th}\)-roots can't.

Also, both of the elementary abelian groups of order 27, and the non-abelian group of order 27 with exponent 3 have similar diagrams (\(\Gamma_n\)'s for \(n=1,2,3\)). So, the above theorem is not true for two arbitrary groups. Of course, it is trivial that, for any isomorphic two groups \(G\) and \(H\) we have \(\Gamma_n(G)\cong\Gamma_n(H)\), for all \(n\).

Finally, with the above remarks in mind, we can ask the following questions:

Question 1. Can we extend theorem 4.1 to some other classes of groups?

Question 2. For a finite group \(G\), what is the minimum number of digraphs of \(n^{th}\)-roots, where \(1\leq n\leq exp(G)\), to characterise it?

References

K. Ahmadidelir, H. Doostie, A. Sadeghieh, Probability that an element of a finite group has an \(n^{th}\)-root. (unpublished)
J. Blum, Enumeration of the square permutations in \(S_n\), J. Combin. Theory (Ser. A), 17 (1974), 156–161.
A. K. Das, On groups elements having square roots, Bull. Iranian Math. Soc., 31, N2 (2005), 33–36.
M. S. Lucido, M. R. Pournaki, Elements with square roots in finite groups, Alg. Colloq. , 12, N4 (2005), 677–690.
N. Pouyanne, On the number of permutations admitting an \(m\)-th root, Electron. J. Combin., 9, N1 (2002), #R3, 12 p. (electronic)