Система QPSLab для анализа и распознавания числовых последовательностей с квазипериодической структурой
ПОСТАНОВКА ПРОБЛЕМЫ
Модель, определения, обозначения
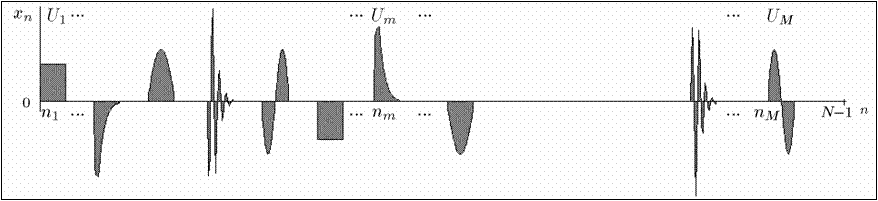
Под числовой последовательностью с квазипериодической структурой подразумевается всякая числовая последовательность, включающая такие фрагменты (подпоследовательности подряд расположенных членов), которые имеют характерные детерминированные или стохастические свойства, причем для всех пар следующих друг за другом фрагментов разность между номерами первых членов последующего и предыдущего фрагментов лежит в фиксированном интервале. Последовательность, имеющая квазипериодическую структуру, или квазипериодическая последовательность ― это последовательность с квазипериодической сменой своих свойств. Например, в случае детерминированной последовательности под сменой свойств понимается изменение формулы общего члена последовательности, а в случае стохастической ― изменение ее вероятностных характеристик.

Числовая последовательность, включающая квазипериодически чередующиеся ненулевые информационные фрагменты размерности q, определяется следующей формулой общего члена:
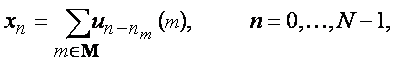
где un-nm (m) = 0, если n-nm ≠ 0,...,q - 1;
0 < ||(u0(m),..., uq-1(m))|| < ∞ при каждом m Î M ={1,...,M}.
Назовем Um = (u0(m),..., uq-1(m)) Î Rq, m Î M, информационным вектором,
(xnm,..., xnm+q-1) Î Rq, m Î M, информационным фрагментом.
Вектор X = X(n1,...,nM, U1,...,UM) функция от двух наборов, (n1,...,nM) и (U1,...,UM).
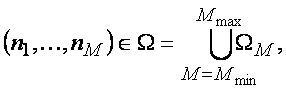
|
ΩM = {(n1,…, nM) | |
0 ≤ n1 ≤ N + ≤ N – q, 0 ≤ N – ≤ nM ≤ N – q, |
| 0 < q ≤ Tmin ≤ nm – nm–1 ≤ Tmax ≤ N – q, m = 2,…,M }, | |
|
|
M Î [Mmin,Mmax]. |
Mmin и Mmax находятся из входящей в определение множества ΩM системы ограничений, в которой N –, N +, Tmin, Tmax – целые числа.
Справедливы следующие оценки для мощности множеств:
| ΩM | = O[(N – q + 1)(Tmax – Tmin + 1)M–1],
| Ω | = O[(N – q + 1)(Mmax – Mmin + 1)(Tmax – Tmin + 1)Mmax–1],
причем M, Mmax – кусочно-постоянные возрастающие функции от N.
Критерий решения задачи
Предполагается, что вектор X = (x0,...,xN-1), последовательность компонент которого включает фрагменты, совпадающие с набором (U1,...,UM) эталонных векторов, недоступен для непосредственой обработки из-за вектора помехи E = (ε0,..., εN-1) Î Φ0,σ2I, где Φ0,σ2I ― нормальное распределение.
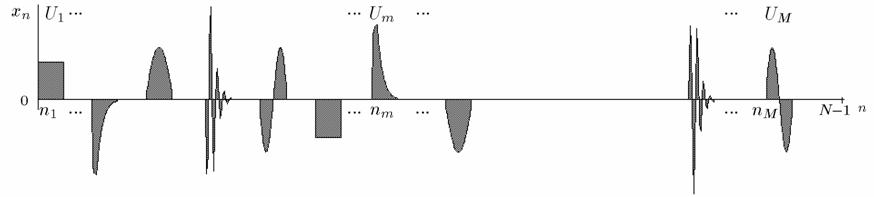
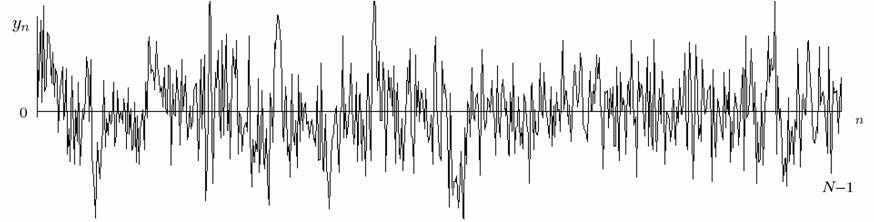
Доступным для обработки, как это проиллюстрировано на рисунке, считается вектор Y = X + E.
Рассматриваемые дискретные экстремальные задачи возникают в результате формализации содержательных задач обработки данных как задач принятия решения (о среднем случайного гауссовского вектора Y Î ), доставляющего максимум функционалу правдоподобия.
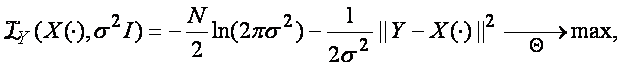
где Θ – множество всевозможных (допустимых) векторов X.
К идентичным формулировкам экстремальных задач приводит минимизация функционала ||Y - X(·) ||2 суммы квадратов уклонений.