- 1)
- если
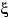 и
и 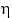 независимы, то
независимы, то
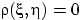 ;
;
- 2)
- всегда
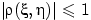 ;
;
- 3)
-
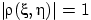 тогда и только тогда, когда
тогда и только тогда, когда
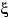 и
и 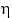 п. н. линейно связаны, т.е.
существуют числа
п. н. линейно связаны, т.е.
существуют числа 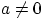 и
и 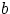 такие, что
такие, что 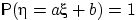 .
.
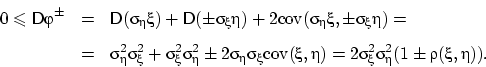
Мы получили два полезных соотношения:
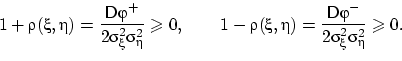 | (20) |
Из них сразу следует, что ![]() .
.
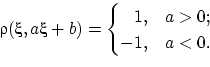
Не забудьте, что ![]() , а не просто
, а не просто ![]() !
!
Докажем вторую часть свойства (3): если ![]() , то
существуют числа
, то
существуют числа ![]() и
и ![]() такие, что
такие, что ![]() .
.
Рассмотрим сначала случай ![]() .
Это возможно только если второе неравенство в формуле (20) превращается в равенство:
.
Это возможно только если второе неравенство в формуле (20) превращается в равенство:
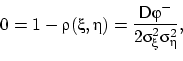
т.е. ![]() . Тогда, по свойству (D3),
. Тогда, по свойству (D3), ![]() п.н., где
п.н., где ![]() — некоторое число.
Иначе говоря,
— некоторое число.
Иначе говоря, ![]() п.н., или
п.н., или
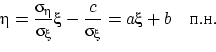
В случае ![]() нужно рассмотреть первое
неравенство в формуле (20) и повторить рассуждения.
Тем самым теорема 31 доказана.
нужно рассмотреть первое
неравенство в формуле (20) и повторить рассуждения.
Тем самым теорема 31 доказана.
QED
Так, величины ![]() и
и ![]() в примерах 49 и 50
положительно коррелированы, но их зависимость не функциональная.
в примерах 49 и 50
положительно коррелированы, но их зависимость не функциональная.
Следующее свойство показывает, что модуль коэффициента корреляции не меняется при линейных преобразованиях случайных величин.
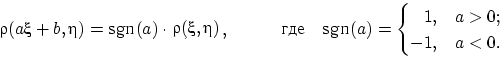
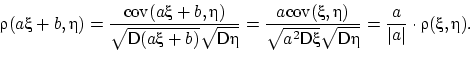
Осталось заметить, что знак ![]() как раз и равен
как раз и равен ![]() .
.
QED
N.Ch.